Leetcode记录：二分查找和双指针法

29 Jul 2024

二分查找

二分查找的前提为有序数组，同时要关注数组是否存在重复元素。

二分查找的框架为

int binarySearch(int[] nums, int target) {
    int left = 0, right = ...;

    while(...) {
        int mid = left + (right - left) / 2;
        if (nums[mid] == target) {
            ...
        } else if (nums[mid] < target) {
            left = ...
        } else if (nums[mid] > target) {
            right = ...
        }
    }
    return ...;
}

分析二分查找的一个技巧是：不要出现 else，而是把所有情况用 else if 写清楚，这样可以清楚地展现所有细节。另外，计算 mid 时需要技巧防止溢出。

基本的二分查找

省略号的部分可以分为两种写法：左闭右闭和左闭右开，可以画图来进行分析，此处略过

int search(vector<int>& nums, int target) {
        int left = 0;
        int right = nums.size() - 1; // 定义target在左闭右闭的区间里，[left, right]
        while (left <= right) { // 当left==right，区间[left, right]依然有效，所以用 <=
            int midd = left + ((right - left) / 2);// 防止溢出 等同于(left + right)/2
            if (nums[mid] > target) {
                right = mid - 1; // target 在左区间，所以[left, middle - 1]
            } else if (nums[mid] < target) {
                left = mid + 1; // target 在右区间，所以[middle + 1, right]
            } else { // nums[middle] == target
                return mid; // 数组中找到目标值，直接返回下标
            }
        }
        // 未找到目标值
        return -1;
    }
// Another version:
int search(vector<int>& nums, int target) {
        int left = 0;
        int right = nums.size(); // 定义target在左闭右开的区间里，即：[left, right)
        while (left < right) { // 因为left == right的时候，在[left, right)是无效的空间，所以使用 <
            int middle = left + ((right - left) >> 1);
            if (nums[middle] > target) {
                right = middle; // target 在左区间，在[left, middle)中
            } else if (nums[middle] < target) {
                left = middle + 1; // target 在右区间，在[middle + 1, right)中
            } else { // nums[middle] == target
                return middle; // 数组中找到目标值，直接返回下标
            }
        }
        // 未找到目标值
        return -1;
    }

但是如果给定有序数组 nums = [1,2,2,2,3]，target = 2，此算法返回的索引是 2，但是如果我想得到 target 的左侧边界，即索引 1，或者我想得到 target 的右侧边界，即索引 3，这样的话此算法是无法处理的。

寻找左右侧边界的二分搜索

int left_bound(vector<int>& nums, int target) {
    if (nums.size() == 0) return -1;
    int left = 0;
    int right = nums.size() -1; // 注意

    while (left <= right) { // 注意
        int mid = (left + right) / 2;
        if (nums[mid] == target) {
            right = mid - 1;
        } else if (nums[mid] < target) {
            left = mid + 1;
        } else if (nums[mid] > target) {
            right = mid - 1; // 注意
        }
    }
    // target 比所有数都大
    if (left == nums.size()) return -1;
    return nums[left] == target ? left : -1;
}

int right_bound(vector<int>& nums, int target) {
    if (nums.size() == 0) return -1;
    int left = 0, right = nums.size()-1;

    while (left <= right) {
        int mid = (left + right) / 2;
        if (nums[mid] == target) {
            left = mid + 1; // 注意
        } else if (nums[mid] < target) {
            left = mid + 1;
        } else if (nums[mid] > target) {
            right = mid -1;
        }
    }
    if (right == -1) return -1;
    return nums[right] == target ? right : -1; // 注意
}

也可以统一写为一个函数

int binarySearch(vector<int>& nums, int target, bool left_bound){
    int left = 0; int right = nums.size()-1;
    while(left <= right){
        int mid = (left + right) / 2;
        if(nums[mid] > target || (lower && nums[mid] >= target)){
            right = mid - 1;
        }else{
            left = mid + 1;
        }
    }
    return left;
}
vector<int> searchRange(vector<int>& nums, int target) {
    int leftIdx = binarySearch(nums, target, true);
    int rightIdx = binarySearch(nums, target, false) - 1;
    if (leftIdx <= rightIdx && rightIdx < nums.size() &&
        nums[leftIdx] == target && nums[rightIdx] == target){
        return vector<int>{leftIdx, rightIdx};
    } 
    return vector<int>{-1, -1};
}

寻找两个中序数组的中位数

Leetcode 4. 给定两个大小分别为 m 和 n 的正序（从小到大）数组 nums1 和 nums2。请你找出并返回这两个正序数组的中位数算法的时间复杂度应该为 O(log (m+n)) 。

这道题可以转化成寻找两个有序数组中的第 k 小的数，其中 k 为 (m+n)/2 或 (m+n)/2+1。 假设两个有序数组分别是 A 和 B。要找到第 k 个元素，我们可以比较 A[k/2−1] 和 B[k/2−1]，对于较小值，最多只会有 k−2 个元素比它小，那么它就不能是第 k 小的数了。

int getKthElement(const vector<int> &nums1, const vector<int> &nums2, int k){
    int m = nums1.size(), n = nums2.size();
    int index1 = 0, index2 = 0;

    while(true){
        if(index1 == m){
            return nums2[index2 + k - 1];
        }
        if(index2 == n){
            return nums1[index1 + k - 1];
        }
        if(k == 1)
            return min(nums1[index1], nums2[index2]);
    
        int newIndex1 = min(index1 + k/2 - 1, m-1);
        int newIndex2 = min(index2 + k/2 - 1, n-1);
        int pivot1 = nums1[newIndex1], pivot2 = nums2[newIndex2];
        if(pivot1 <= pivot2){
            k-= newIndex1 - index1 + 1;
            index1 = newIndex1 + 1;
        } else{
            k -= newIndex2 - index2 + 1;
            index2 = newIndex2 + 1;
        }
    }
}
double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
    int totalLength = nums1.size() + nums2.size();
    if(totalLength % 2 == 1)
        return getKthElement(nums1, nums2, (totalLength+1)/2);
    else
        return (getKthElement(nums1,nums2,totalLength/2) + getKthElement(nums1, nums2, totalLength/2+1)) / 2.0;
}

对应题目：

704.二分查找
35.搜索插入位置
34.在排序数组中查找元素的第一个和最后一个位置

双指针法

双指针是指在遍历对象的过程中，不是普通的使用单个指针进行访问，而是使用两个指针进行遍历，从而达到相应的目的。

最常见的双指针算法有两种：

在同一个序列中，用两个指针维护两个位置，或两个位置包含的区间；
在两个序列里边，两个指针指向不同的序列，来维护某种次序。

按照指针的移动方向，双指针分为同向双指针、异向双指针：

同向双指针，也称快慢指针（两个指针一快一慢）；
异向双指针，分为对撞指针（从两边向中间移动）、背向指针（从中间向两边移动）。

快慢指针

两个指针，初始在同一位置，然后向相同方向移动，一个移动速度快，一个移动速度慢。

适用场景：查找链表中间节点、链表是否包含环、原地修改数组。

示例1

LeetCode 876.【链表的中间结点】

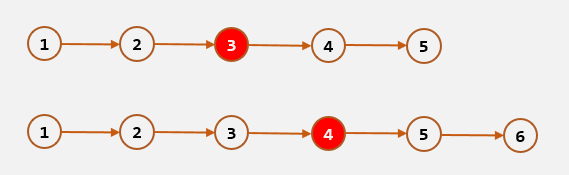
给你单链表的头结点 head ，请你找出并返回链表的中间结点。如果有两个中间结点，则返回第二个中间结点。如下图所示，链表有 5 个节点，返回第 3 个节点；链表有 6 个节点，返回第 4 个节点。

ListNode middleNode(ListNode head) {
    ListNode fast = head;
    ListNode slow = head;
    while (fast != null && fast.next != null) {
        fast = fast.next.next;
        slow = slow.next;
    }
    return slow;
}

示例2

LeetCode 26.【删除有序数组中的重复项】给你一个非严格递增排列的数组 nums ，请你原地删除重复出现的元素，使每个元素只出现一次，返回删除后数组的新长度。元素的相对顺序应该保持一致。然后返回 nums 中唯一元素的个数。

int removeElement(vector<int>& nums, int val) {
    int slowIndex=0;
    for(int fastIndex =0;fastIndex<nums.size();fastIndex++)
    {
        if(val!=nums[fastIndex])
        {
            nums[slowIndex++]=nums[fastIndex];
        }
    }
    return slowIndex;
}

对撞指针

两个指针，初始一个在左、一个在右，左指针向右移动，右指针向左移动，直到相撞停止。

适用场景：二分查找、反转数组、回文判定。

示例1

LeetCode 977.【有序数组的平方】给你一个按非递减顺序排序的整数数组 nums，返回每个数字的平方组成的新数组，要求也按非递减顺序排序。

由于数组平方的最大值就在数组的两端，不是最左边就是最右边，不可能是中间，此时可以考虑双指针法了

vector<int> sortedSquares(vector<int>& A) {
        int k = A.size() - 1;
        vector<int> result(A.size(), 0);
        for (int i = 0, j = A.size() - 1; i <= j;) { // 注意这里要i <= j，因为最后要处理两个元素
            if (A[i] * A[i] < A[j] * A[j])  {
                result[k--] = A[j] * A[j];
                j--;
            }
            else {
                result[k--] = A[i] * A[i];
                i++;
            }
        }
        return result;
    }

示例2

LeetCode 344.【反转字符串】

编写一个函数，其作用是将输入的字符串反转过来。输入字符串以字符数组 s 的形式给出。不要给另外的数组分配额外的空间，你必须原地修改输入数组、使用 O(1) 的额外空间解决这一问题。

void reverseString(char[] s) {
    int left = 0;
    int right = s.length - 1;
    while (left < right) {
        char tmp = s[left];
        s[left] = s[right];
        s[right] = tmp;
        left++;
        right--;
    }
}

背向指针

两个指针，初始都在中间，左指针向左移动，右指针向右移动，直至碰到最左或最右边界。

使用场景：查找字符串中的最长回文子串。

示例1

LeetCode 5.最长回文子串

给你一个字符串 s，找到 s 中最长的回文子串。如果字符串的反序与原始字符串相同，则该字符串称为回文字符串。

在给定字符串中找回文子串的难点在于，回文子串的的长度可能是奇数也可能是偶数，如果回文串的长度为奇数，则它有一个中心字符，例如bacab；如果回文串的长度为偶数，则可以认为它有两个中心字符，例如baab。

string expandCenter(string s, int left, int right) {
    int len = s.length();
    // 要时刻注意避免越界访问
    while (left >= 0 && right < len
           && s[left] == s[right]) {
        left--;
        right++;
    }
    return s.substr(left + 1, right - left - 1);
}

string longestPalindrome(string s) {
    int len = s.length();
    string res;
    for (int i = 0; i < len; i++) {
        string sub1 = expandCenter(s, i, i);
        string sub2 = expandCenter(s, i, i + 1);
        res = res.length() >= sub1.length() ? res : sub1;
        res = res.length() >= sub2.length() ? res : sub2;
    }
    return res;
}

数据结构与算法