Leetcode记录：滑动窗口和前缀和

31 Jul 2024

滑动窗口

滑动窗口算法的基本思想是维护一个窗口，通过移动窗口的两个边界来处理问题。

具体来说，我们可以使用两个指针 left 和 right 分别表示滑动窗口的左右边界，然后通过不断移动右指针 right 来扩大窗口，同时根据问题的要求调整左指针 left 来缩小窗口。当右指针 right 扫描到字符串或数组的末尾时，算法的执行就完成了。

在扩大或缩小窗口的过程中，可以记录下一些中间结果，例如最大值、最小值、子串长度等等，从而求解问题的最终答案。

适用问题

滑动窗口算法可以用于解决一些字符串和数组问题，例如：

字符串匹配问题，例如 Leetcode 第 28 题和第 76 题；
最长子串或子数组问题，例如 Leetcode 第 3 题、第 209 题和第 424 题；
最小覆盖子串问题，例如 Leetcode 第 76 题；
字符串排列问题，例如 Leetcode 第 567 题；
求解字符串或数组中的一些性质，例如 Leetcode 第 438 题、第 567 题和第 1004 题等。

实现方法

滑动窗口算法的实现方法相对简单，主要分为以下几个步骤：

初始化左右指针 $left$ 和 $right$，并根据问题的要求进行一些初始化操作。
不断移动右指针 $right$，直到出现不符合条件的情况，或者扫描到字符串或数组的末尾。
对于每个右指针位置 $i$，更新一些中间结果。
移动左指针 $left$，直到出现符合条件的情况，或者左右指针重合。
重复第 2 步至第 4 步，直到右指针扫描到字符串或数组的末尾。

示例1

Leetcode 206.【长度最小的子数组】给定一个含有 n 个正整数的数组和一个正整数 target 。找出该数组中满足其总和大于等于 target 的长度最小的子数组[numsl, numsl+1, ..., numsr-1, numsr] ，并返回其长度。如果不存在符合条件的子数组，返回 0 。

这道题之所以可以使用滑动窗口，很重要的一个原因是，在移动终止位置的时候，初始位置是不可逆的，初始位置只可能往后移动，而不用每次都从第零个元素开始。 代码实现如下：

int minSubArrayLen(int s, vector<int>& nums) {
        int result = INT32_MAX;
        int sum = 0; // 滑动窗口数值之和
        int i = 0; // 滑动窗口起始位置
        int subLength = 0; // 滑动窗口的长度
        for (int j = 0; j < nums.size(); j++) {
            sum += nums[j];
            // 注意这里使用while，每次更新 i（起始位置），并不断比较子序列是否符合条件
            while (sum >= s) {
                subLength = (j - i + 1); // 取子序列的长度
                result = result < subLength ? result : subLength;
                sum -= nums[i++]; // 这里体现出滑动窗口的精髓之处，不断变更i（子序列的起始位置）
            }
        }
        // 如果result没有被赋值的话，就返回0，说明没有符合条件的子序列
        return result == INT32_MAX ? 0 : result;
    }

示例2

Leetcode 3.【无重复最长子串】给定一个字符串 s ，请你找出其中不含有重复字符的最长子串的长度。

int lengthOfLongestSubstring(string s) {
    int n = s.size();
    int ans = 0;
    unordered_map<char, int> map;//记录字符上一次出现的位置,字符为key，位置为value
    for(int i = 0, j = 0; j < n; j++){//i表示子串的起始位置，j表示子串的结束位置
        if(map.find(s[j]) != map.end()){//如果字符上一次出现的位置在i之后，更新i
            i = max(map[s[j]], i);//map[s[j]]表示字符s[j]上一次出现的位置
        }
        ans = max(ans, j - i + 1);//更新结果
        map[s[j]] = j + 1;		//更新字符s[j]上一次出现的位置
    }
    return ans;
}

示例3

Leetcode 1004.【最大连续1的个数】

给定一个二进制数组 nums 和一个整数 k，如果可以翻转最多 k 个0 ，则返回数组中连续 1 的最大个数。

int longestOnes(vector<int>& nums, int k) {
    int n = nums.size();
    int left = 0, lsum = 0, rsum = 0;
    int ans = 0;
    for (int right = 0; right < n; ++right) {
        rsum += 1 - nums[right]; //[0，right]中0的个数.
        while (lsum < rsum - k) {
            lsum += 1 - nums[left];
            ++left;
        }
        ans = max(ans, right - left + 1);
    }
    return ans;
}

该问题也可以用前缀和思路来考虑：要想快速判断一个区间内 0 的个数，我们可以考虑将数组中的 0 变成 1，1 变成 0。此时，我们对数组 A 求出前缀和，记为数组 P，那么 [left,right] 中包含不超过 k 个 1（注意这里就不是 0 了），当且仅当二者的前缀和之差：P[right]−P[left−1]<=k.

int longestOnes(vector<int>& nums, int k) {
    int n = nums.size();
    vector<int> P(n + 1);
    for (int i = 1; i <= n; ++i) {
        P[i] = P[i - 1] + (1 - nums[i - 1]);
    }

    int ans = 0;
    for (int right = 0; right < n; ++right) {
        int left = lower_bound(P.begin(), P.end(), P[right + 1] - k) - P.begin();
        ans = max(ans, right - left + 1);
    }
    return ans;
    }

其中 lower_bound 用于在有序序列中查找第一个大于或等于给定值的元素的位置（迭代器）。

示例4 等二刷用优化再做一遍

Leetcode 76.【最小覆盖子串】给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串，则返回空字符串 "" 。

unordered_map<char,int> ori, cnt;
    
bool check() {
    for (const auto &p : ori) {
        if (cnt[p.first] < p.second) {
            return false;
        }
    }
    return true;
}

string minWindow(string s, string t) {
    for (auto & c : t){
        ori[c]++;
    }
    int length = INT_MAX;
    int left = 0;
    int right = 0; 
    int ansLeft = 0;
    while (right <= s.length()) {
        if (ori.find(s[right]) != ori.end()) {
            cnt[s[right]]++;
        }
        while (check() && left <=right) {
            if (right - left + 1 < length){
                ansLeft = left;
                length = right - left + 1;
            }
            if (ori.find(s[left])!= ori.end()) {
                cnt[s[left]]--;
            }
            left++;
        }
        right++;
    }
    return length == INT_MAX ? "" : s.substr(ansLeft, length);
}

注意更新右端窗口及cnt的时候先移动左端窗口，更新length，最后再right++.

优化算法： 用一个变量 less 维护目前子串中有 less 种字母的出现次数小于 t 中字母的出现次数。具体来说（注意下面算法中的 less 变量）：

初始化 ansLeft=−1, ansRight=m，用来记录最短子串的左右端点，其中 m 是 s 的长度。
用一个哈希表（或者数组）cntT 统计 t 中每个字母的出现次数。
初始化 left=0，以及一个空哈希表（或者数组）cntS，用来统计 s 子串中每个字母的出现次数。
初始化 less 为 t 中的不同字母个数。
遍历 s，设当前枚举的子串右端点为 right，把字母 c=s[right] 的出现次数加一。加一后，如果 cntS[c]=cntT[c]，说明 c 的出现次数满足要求，把 less 减一。
如果 less=0，说明 cntS 中的每个字母及其出现次数都大于等于 cntT 中的字母出现次数，那么：如果 right−left < ansRight−ansLeft，说明我们找到了更短的子串，更新 ansLeft=left, ansRight=right。
把字母 x=s[left] 的出现次数减一。减一前，如果 cntS[x]=cntT[x]，说明 x 的出现次数不满足要求，把 less 加一。
左端点右移，即 left 加一。
重复上述三步，直到 less>0，即 cntS 有字母的出现次数小于 cntT 中该字母的出现次数为止。
最后，如果 ansLeft<0，说明没有找到符合要求的子串，返回空字符串，否则返回下标 ansLeft 到下标 ansRight 之间的子串。

string minWindow(string s, string t) {
        int m = s.length();
        int ans_left = -1, ans_right = m, left = 0, less = 0;
        int cnt_s[128]{}, cnt_t[128]{};
        for (char c : t) {
            less += cnt_t[c]++ == 0; // 有 less 种字母的出现次数 < t 中的字母出现次数
        }
        for (int right = 0; right < m; right++) { // 移动子串右端点
            char c = s[right]; // 右端点字母（移入子串）
            less -= ++cnt_s[c] == cnt_t[c]; // c 的出现次数从 < 变成 >=
            while (less == 0) { // 涵盖：所有字母的出现次数都是 >=
                if (right - left < ans_right - ans_left) { // 找到更短的子串
                    ans_left = left; // 记录此时的左右端点
                    ans_right = right;
                }
                char x = s[left++]; // 左端点字母（移出子串）
                less += cnt_s[x]-- == cnt_t[x]; // x 的出现次数从 >= 变成 <
            }
        }
        return ans_left < 0 ? "" : s.substr(ans_left, ans_right - ans_left + 1);
    }

示例5

Leetcode 904.【水果成篮】实质上就是找最多包含$k$个元素的连续最长子数组。

int totalFruit(vector<int>& fruits) {
        int n = fruits.size();
        unordered_map<int, int> cnt;

        int left = 0, ans = 0;
        for (int right = 0; right < n; ++right) {
            ++cnt[fruits[right]];
            while (cnt.size() > 2) {
                auto it = cnt.find(fruits[left]);
                --it->second;
                if (it->second == 0) {
                    cnt.erase(it);
                }
                ++left;
            }
            ans = max(ans, right - left + 1);
        }
        return ans;
    }

可以发现，滑动窗口和最大最小子数组或字符串问题关系密切，更新左窗口和更新length的先后顺序与最大还是最小问题相关

找出字符串中所有字母的异位词

Leetcode 438. 给定两个字符串 s 和 p，找到 s 中所有 p 的异位词的子串，返回这些子串的起始索引。不考虑答案输出的顺序。

我们可以在字符串 s 中构造一个长度为与字符串 p 的长度相同的滑动窗口，并在滑动中维护窗口中每种字母的数量；当窗口中每种字母的数量与字符串 p 中每种字母的数量相同时，则说明当前窗口为字符串 p 的异位词。

在此基础上，我们不再分别统计滑动窗口和字符串 p 中每种字母的数量，而是统计滑动窗口和字符串 p 中每种字母数量的差；并引入变量 differ 来记录当前窗口与字符串 p 中数量不同的字母的个数，并在滑动窗口的过程中维护它。在判断滑动窗口中每种字母的数量与字符串 p 中每种字母的数量是否相同时，只需要判断 differ 是否为零即可。

vector<int> findAnagrams(string s, string p) {
    int sLen = s.size(), pLen = p.size();
    if (sLen < pLen)
        return vector<int>{};
    vector<int> ans;
    vector<int> count(26);
    for(int i = 0; i < pLen; ++i){
        ++count[s[i]-'a'];
        --count[p[i]-'a'];
    }
    int differ = 0;
    for(int i = 0; i < 26; ++i){
        if(count[i]!=0)
            ++differ;
    }
    if (differ == 0) {
        ans.push_back(0);
    }
    for(int i = 0; i < sLen-pLen; ++i) {
        if (count[s[i]-'a'] == 1){
            --differ;
        } else if(count[s[i]-'a'] == 0){
            ++differ;
        }
        --count[s[i]-'a'];

        if (count[s[i+pLen]-'a'] == -1){
            --differ;
        } else if(count[s[i+pLen]-'a'] == 0){
            ++differ;
        }
        ++count[s[i+pLen]-'a'];

        if(differ == 0)
            ans.push_back(i+1);
    }
    return ans;
}

串联所有单词的子串

Leetcode 30. 给定一个字符串 s 和一个字符串数组 words。 words中所有字符串长度相同。 s 中的串联子串是指一个包含 words 中所有字符串以任意顺序排列连接起来的子串。返回所有串联子串在 s 中的开始索引。

和上一道题十分类似，只不过字符变成了单词，记 words 的长度为 m，words 中每个单词的长度为 n，s 的长度为 ls。首先需要将 s 划分为单词组，每个单词的大小均为 n （首尾除外）。这样的划分方法有 n 种，即先删去前 i （i=0∼n−1）个字母后，将剩下的字母进行划分，如果末尾有不到 n 个字母也删去。对这 n 种划分得到的单词数组分别使用滑动窗口对 words 进行类似于「字母异位词」的搜寻。

vector<int> findSubstring(string &s, vector<string> &words) {
    vector<int> res;
    int m = words.size(), n = words[0].size(), ls = s.size();
    for (int i = 0; i < n && i + m * n <= ls; ++i) {
        unordered_map<string, int> differ;
        for (int j = 0; j < m; ++j) {
            ++differ[s.substr(i + j * n, n)];
        }
        for (string &word: words) {
            if (--differ[word] == 0) {
                differ.erase(word);
            }
        }
        for (int start = i; start < ls - m * n + 1; start += n) {
            if (start != i) {
                string word = s.substr(start + (m - 1) * n, n);
                if (++differ[word] == 0) {
                    differ.erase(word);
                }
                word = s.substr(start - n, n);
                if (--differ[word] == 0) {
                    differ.erase(word);
                }
            }
            if (differ.empty()) {
                res.emplace_back(start);
            }
        }
    }
    return res;
}

字符串的排列

Leetcode 567. 给你两个字符串 s1 和 s2 ，写一个函数来判断 s2 是否包含 s1 的排列。如果是，返回 true ；否则，返回 false 。

用前面的方法直接解决。

前缀和

前缀和算法（Prefix Sum）是一种用于快速计算数组元素之和的技术。它通过预先计算数组中每个位置前所有元素的累加和，将这些部分和存储在一个新的数组中，从而在需要计算某个区间的和时，可以通过简单的减法操作得到结果，而不必重新遍历整个区间。

一维前缀和：给定一个整数数组 Array，请计算该数组在每个指定区间内元素的总和。

int main() {
    int n, a, b;
    cin >> n;
    vector<int> vec(n);
    vector<int> p(n);
    int presum = 0;
    for (int i = 0; i < n; i++) {
        cin >> vec[i];
        presum += vec[i];
        p[i] = presum;
    }

    while (cin >> a >> b) {
        int sum;
        if (a == 0) sum = p[b];
        else sum = p[b] - p[a - 1];
        cout << sum << endl;
    }
}

二维前缀和：给你一个n行m列的矩阵A ，下标从1开始。 请输出以 (x1, y1) 为左上角 , (x2,y2) 为右下角的子矩阵的和。

int main() 
{
    int n = 0, m = 0
    cin >> n >> m;
    vector<vector<int>> arr(n + 1, vector<int>(m + 1));
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++)
            cin >> arr[i][j];
 
    vector<vector<long long>> dp(n + 1, vector<long long>(m + 1));
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++)
            dp[i][j] = dp[i-1][j] + dp[i][j-1] + arr[i][j] - dp[i-1][j-1]; //注意这一步.
 
    int x1 = 0, y1 = 0, x2 = 0, y2 = 0;
    while (cin >> x1 >> y1 >> x2 >> y2;)
    {
        cout << dp[x2][y2] - dp[x1-1][y2] - dp[x2][y1-1] + dp[x1-1][y1-1] << endl;
    }
 
    return 0;
}

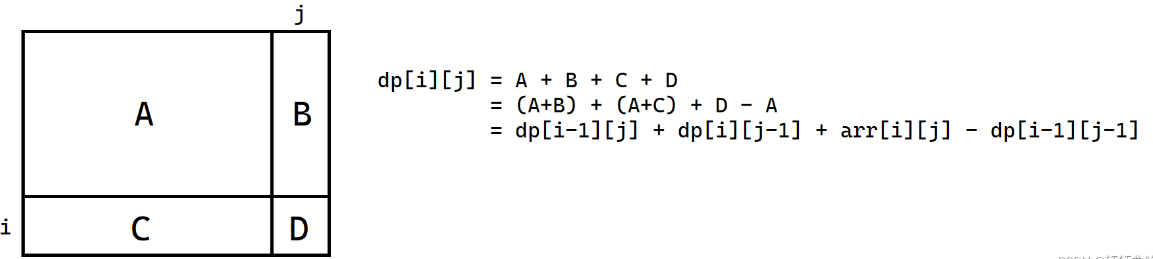
示例1

Leetcode 238.【除自身以外数组的乘积】给你一个整数数组 nums，返回数组 answer ，其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积。

vector<int> productExceptSelf(vector<int>& nums) {
    int length = nums.size();
    vector<int> answer(length);

    // answer[i] 表示索引 i 左侧所有元素的乘积
    // 因为索引为 '0' 的元素左侧没有元素， 所以 answer[0] = 1
    answer[0] = 1;
    for (int i = 1; i < length; i++) {
        answer[i] = nums[i - 1] * answer[i - 1];
    }

    // R 为右侧所有元素的乘积
    // 刚开始右边没有元素，所以 R = 1
    int R = 1;
    for (int i = length - 1; i >= 0; i--) {
        // 对于索引 i，左边的乘积为 answer[i]，右边的乘积为 R
        answer[i] = answer[i] * R;
        // R 需要包含右边所有的乘积，所以计算下一个结果时需要将当前值乘到 R 上
        R *= nums[i];
    }
    return answer;
}

示例2

Leetcode 560.【和为k的子数组】给你一个整数数组 nums 和一个整数 k ，请你统计并返回该数组中和为 k 的子数组的个数。

由于数组可能存在负数，我们无法使用滑动窗口来求解该问题。我们可以存储所有的前缀和出现的次数，遍历的时候寻找 pre-k 的个数即可。

int subarraySum(vector<int>& nums, int k) {
        unordered_map<int, int> mp;
        mp[0] = 1; //注意！
        int count = 0, pre = 0;
        for (auto& x:nums) {
            pre += x;
            if (mp.find(pre - k) != mp.end()) {
                count += mp[pre - k];
            }
            mp[pre]++;
        }
        return count;
    }

示例3

Leetcode 974. 【和可被K整除的子数组】给定一个整数数组 nums 和一个整数 k，返回其中元素之和可被 k 整除的非空子数组的数目。

由于负数的存在，这里我们存储的是 (pre % k + k) % k的个数，

int subarraysDivByK(vector<int>& nums, int k) 
{
    int ret = 0;
    unordered_map<int, int> hash;
    hash[0] = 1;

    int sum = 0;
    for (auto e : nums)
    {
        sum += e;
        int mod = (sum % k + k) % k; //这里考虑有负数的情况
        if (hash.count(mod)) ret += hash[mod];
        hash[mod]++;
    }

    return ret;
}

示例4

Leetcode 525.【连续数组】给定一个二进制数组 nums , 找到含有相同数量的 0 和 1 的最长连续子数组，并返回该子数组的长度。

这里的技巧是将0替换为-1，这样只需求和为0的最长连续子数组。我们要想知道区间长度，就需要知道i和j，因此我们向哈希表中存入的value为当前前缀和的下标。此外，如果我们再次遇到一个值为sum的下标，由于这里求得是最长区间，所以我们不需要更新hash[sum]。而如果整个区间的长度都为0，那么我们就需要在前缀和为0的情况下，找到一个下标为-1的地方来统计整个数组长度。

int findMaxLength(vector<int>& nums) 
{
    for (auto& e : nums) if (e == 0) e = -1;
    unordered_map<int, int> hash;
    hash[0] = -1;

    int ret = 0;
    int sum = 0;
    for (int i = 0; i < nums.size(); i++)
    {
        sum += nums[i];
        if (hash.count(sum)) ret = max(ret, i - hash[sum]);
        else hash[sum] = i;
    }

    return ret;
}

数据结构与算法