Leetcode记录：链表

1 Aug 2024

理解虚拟头结点

考虑单链表删除某一结点的操作，在单链表中移除头结点和移除其他节点的操作方式是不一样的，需要单独写一段逻辑来处理移除头结点的情况。此时就要使用到虚拟头结点，可以保证逻辑的一致性：

ListNode* removeElements(ListNode* head, int val) {
    ListNode* dummyHead = new ListNode(0); // 设置一个虚拟头结点
    dummyHead->next = head; // 将虚拟头结点指向head，这样方便后面做删除操作
    ListNode* cur = dummyHead;
    while (cur->next != NULL) {
        if(cur->next->val == val) {
            ListNode* tmp = cur->next;
            cur->next = cur->next->next;
            delete tmp;
        } else {
            cur = cur->next;
        }
    }
    head = dummyHead->next;
    delete dummyHead;
    return head;
}

设计链表

Leetcode 707. 在链表类中实现这些功能：

get(index)：获取链表中第 index 个节点的值。如果索引无效，则返回-1。
addAtHead(val)：在链表的第一个元素之前添加一个值为 val 的节点。插入后，新节点将成为链表的第一个节点。
addAtTail(val)：将值为 val 的节点追加到链表的最后一个元素。
addAtIndex(index,val)：在链表中的第 index 个节点之前添加值为 val 的节点。如果 index 等于链表的长度，则该节点将附加到链表的末尾。如果 index 大于链表长度，则不会插入节点。如果index小于0，则在头部插入节点。
deleteAtIndex(index)：如果索引 index 有效，则删除链表中的第 index 个节点。

可以发现，使用虚拟头结点之后可以减少逻辑判断.

class MyLinkedList {
public:
    // 定义链表节点结构体
    struct LinkedNode {
        int val;
        LinkedNode* next;
        LinkedNode(int val):val(val), next(nullptr){}
    };

    // 初始化链表
    MyLinkedList() {
        _dummyHead = new LinkedNode(0); // 这里定义的头结点 是一个虚拟头结点，而不是真正的链表头结点
        _size = 0;
    }

    // 获取到第index个节点数值，如果index是非法数值直接返回-1， 注意index是从0开始的，第0个节点就是头结点
    int get(int index) {
        if (index > (_size - 1) || index < 0) {
            return -1;
        }
        LinkedNode* cur = _dummyHead->next;
        while(index--){ // 如果--index 就会陷入死循环
            cur = cur->next;
        }
        return cur->val;
    }

    // 在链表最前面插入一个节点，插入完成后，新插入的节点为链表的新的头结点
    void addAtHead(int val) {
        LinkedNode* newNode = new LinkedNode(val);
        newNode->next = _dummyHead->next;
        _dummyHead->next = newNode;
        _size++;
    }

    // 在链表最后面添加一个节点
    void addAtTail(int val) {
        LinkedNode* newNode = new LinkedNode(val);
        LinkedNode* cur = _dummyHead;
        while(cur->next != nullptr){
            cur = cur->next;
        }
        cur->next = newNode;
        _size++;
    }

    // 在第index个节点之前插入一个新节点，例如index为0，那么新插入的节点为链表的新头节点。
    // 如果index 等于链表的长度，则说明是新插入的节点为链表的尾结点
    // 如果index大于链表的长度，则返回空
    // 如果index小于0，则在头部插入节点
    void addAtIndex(int index, int val) {

        if(index > _size) return;
        if(index < 0) index = 0;        
        LinkedNode* newNode = new LinkedNode(val);
        LinkedNode* cur = _dummyHead;
        while(index--) {
            cur = cur->next;
        }
        newNode->next = cur->next;
        cur->next = newNode;
        _size++;
    }

    // 删除第index个节点，如果index 大于等于链表的长度，直接return，注意index是从0开始的
    void deleteAtIndex(int index) {
        if (index >= _size || index < 0) {
            return;
        }
        LinkedNode* cur = _dummyHead;
        while(index--) {
            cur = cur ->next;
        }
        LinkedNode* tmp = cur->next;
        cur->next = cur->next->next;
        delete tmp;
        //delete命令指示释放了tmp指针原本所指的那部分内存，
        //被delete后的指针tmp的值（地址）并非就是NULL，而是随机值。也就是被delete后，
        //如果不再加上一句tmp=nullptr,tmp会成为乱指的野指针
        //如果之后的程序不小心使用了tmp，会指向难以预想的内存空间
        tmp=nullptr;
        _size--;
    }

    // 打印链表
    void printLinkedList() {
        LinkedNode* cur = _dummyHead;
        while (cur->next != nullptr) {
            cout << cur->next->val << " ";
            cur = cur->next;
        }
        cout << endl;
    }
private:
    int _size;
    LinkedNode* _dummyHead;

};

反转链表

Leetcode 206. 给你单链表的头节点 head ，请你反转链表，并返回反转后的链表。

双指针法：

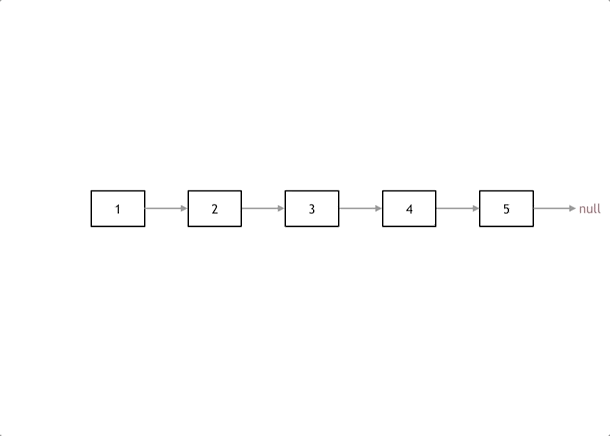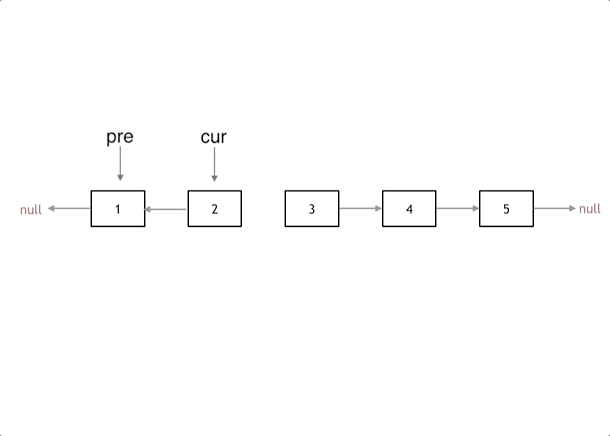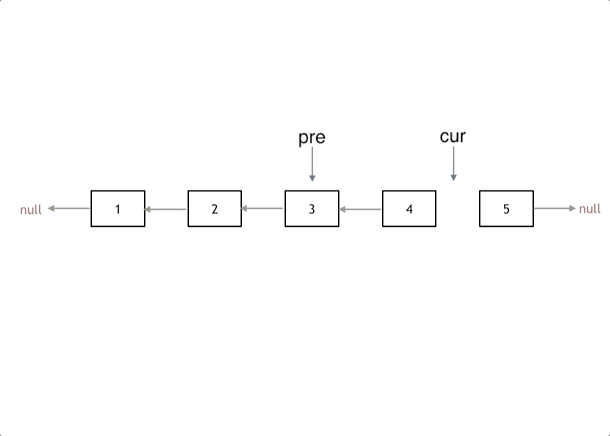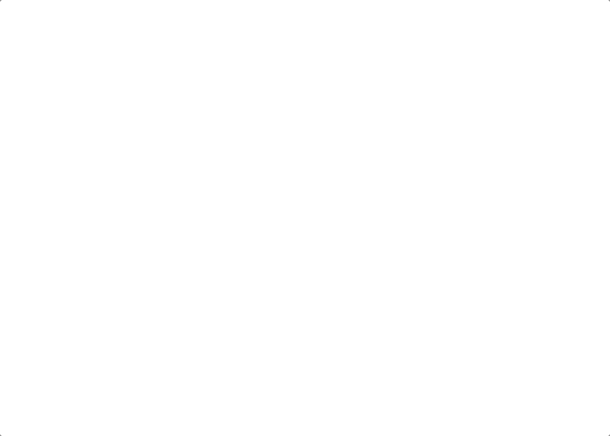
ListNode* reverseList(ListNode* head) {
    ListNode* temp; // 保存cur的下一个节点
    ListNode* cur = head;
    ListNode* pre = NULL;
    while(cur) {
        temp = cur->next;  // 保存一下 cur的下一个节点，因为接下来要改变cur->next
        cur->next = pre; // 翻转操作
        // 更新pre 和 cur指针
        pre = cur;
        cur = temp;
    }
    return pre;
}

递归法：让cur指向pre，然后再将cur与cur->next进行调换。本质上和双指针法相同。

ListNode* reverse(ListNode* pre,ListNode* cur){
    if(cur == NULL) return pre;
    ListNode* temp = cur->next;
    cur->next = pre;
    // 可以和双指针法的代码进行对比，如下递归的写法，其实就是做了这两步
    // pre = cur;
    // cur = temp;
    return reverse(cur,temp);
}
ListNode* reverseList(ListNode* head) {
    // 和双指针法初始化是一样的逻辑
    // ListNode* cur = head;
    // ListNode* pre = NULL;
    return reverse(NULL, head);
}

K个一组反转链表

pair<ListNode*,ListNode*> reverse(ListNode*head, ListNode *tail){
    ListNode *pre = tail->next;
    ListNode *p = head;
    while (pre != tail){
        ListNode *tmp = p->next; 
        p->next = pre;
        pre = p;
        p = tmp;
    }
    return {tail, head};
}
    
ListNode* reverseKGroup(ListNode* head, int k) {
    ListNode *dummyhead = new ListNode(0, head);
    ListNode *pre = dummyhead;
    while(head) {
        ListNode *tail = pre;
        for (int i = 0; i < k; ++i){
            tail = tail-> next;
            if (!tail){
                return dummyhead->next;
            }
        }
        ListNode *tmp =tail->next;
        tie(head, tail) = reverse(head, tail);
        pre->next = head;
        // tail->next = tmp;
        pre = tail;
        head = tmp;
    }
    return dummyhead->next;
}

两两交换链表中的节点

给定一个链表，两两交换其中相邻的节点，并返回交换后的链表。

可以递归可以迭代，使用虚拟头结点避免额外的表头判断。

ListNode* swapPairs(ListNode* head) {
    ListNode* dummyHead = new ListNode(0); // 设置一个虚拟头结点
    dummyHead->next = head; // 将虚拟头结点指向head，这样方便后面做删除操作
    ListNode* cur = dummyHead;
    while(cur->next != nullptr && cur->next->next != nullptr) {
        ListNode* tmp = cur->next; // 记录临时节点
        ListNode* tmp1 = cur->next->next->next; // 记录临时节点

        cur->next = cur->next->next;    // 步骤一
        cur->next->next = tmp;          // 步骤二
        cur->next->next->next = tmp1;   // 步骤三

        cur = cur->next->next; // cur移动两位，准备下一轮交换
    }
    ListNode* result = dummyHead->next;
    delete dummyHead;
    return result;
}

ListNode* swapPairs(ListNode* head) {
    if (head == nullptr || head->next == nullptr)
        return head;
    ListNode *tmp = head->next->next;
    ListNode *p = head->next;
    p->next = head;
    head->next = swapPairs(tmp);
    return p;
}

删除链表倒数第n个节点

给你一个链表，删除链表的倒数第 n 个结点，并且返回链表的头结点。

最简单的方法是先计算总长度再做删除，另外还有两种优化方法：

我们可以使用两个指针 first 和 second 同时对链表进行遍历，并且 first 比 second 超前 n 个节点。当 first 遍历到链表的末尾时，second 就恰好处于倒数第 n 个节点。

 ListNode* removeNthFromEnd(ListNode* head, int n) {
     ListNode* dummy = new ListNode(0, head);
     ListNode* first = head;
     ListNode* second = dummy;
     for (int i = 0; i < n; ++i) {
         first = first->next;
     }
     while (first) {
         first = first->next;
         second = second->next;
     }
     second->next = second->next->next;
     ListNode* ans = dummy->next;
     delete dummy;
     return ans;
 }

可以在遍历链表的同时将所有节点依次入栈。根据栈「先进后出」的原则，我们弹出栈的第 n 个节点就是需要删除的节点，并且目前栈顶的节点就是待删除节点的前驱节点。

 ListNode* removeNthFromEnd(ListNode* head, int n) {
     ListNode* dummy = new ListNode(0, head);
     stack<ListNode*> stk;
     ListNode* cur = dummy;
     while (cur) {
         stk.push(cur);
         cur = cur->next;
     }
     for (int i = 0; i < n; ++i) {
         stk.pop();
     }
     ListNode* prev = stk.top();
     prev->next = prev->next->next;
     ListNode* ans = dummy->next;
     delete dummy;
     return ans;
 }

链表相交

给你两个单链表的头节点 headA 和 headB ，请你找出并返回两个单链表相交的起始节点。如果两个链表没有交点，返回 null 。

一种方法是首先遍历链表 headA，并将链表 headA 中的每个节点加入哈希集合中。然后遍历链表 headB，对于遍历到的每个节点，判断该节点是否在哈希集合中即可：

ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
        unordered_set<ListNode *> visited;
        ListNode *temp = headA;
        while (temp != nullptr) {
            visited.insert(temp);
            temp = temp->next;
        }
        temp = headB;
        while (temp != nullptr) {
            if (visited.count(temp)) {
                return temp;
            }
            temp = temp->next;
        }
        return nullptr;
    }

另一种方法为双指针法：当链表 headA 和 headB 都不为空时，创建两个指针 pA 和 pB，初始时分别指向两个链表的头节点 headA 和 headB，然后将两个指针依次遍历两个链表的每个节点。具体做法如下：

每步操作需要同时更新指针 pA 和 pB。
如果指针 pA 不为空，则将指针 pA 移到下一个节点；如果指针 pB 不为空，则将指针 pB 移到下一个节点。
如果指针 pA 为空，则将指针 pA 移到链表 headB 的头节点；如果指针 pB 为空，则将指针 pB 移到链表 headA 的头节点。
当指针 pA 和 pB 指向同一个节点或者都为空时，返回它们指向的节点或者 null。

假设链表 headA 的不相交部分有 a 个节点，链表 headB 的不相交部分有 b 个节点，两个链表相交的部分有 c 个节点，则有 a+c=m，b+c=n。如果 a=b，则两个指针会同时到达两个链表相交的节点，此时返回相交的节点；如果 a!=b，两个指针不会同时到达链表的尾节点，在指针 pA 移动了 a+c+b 次、指针 pB 移动了 b+c+a 次之后，两个指针会同时到达两个链表相交的节点，该节点也是两个指针第一次同时指向的节点，此时返回相交的节点。

ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
        if (headA == nullptr || headB == nullptr) {
            return nullptr;
        }
        ListNode *pA = headA, *pB = headB;
        while (pA != pB) {
            pA = pA == nullptr ? headB : pA->next;
            pB = pB == nullptr ? headA : pB->next;
        }
        return pA;
    }

环形链表

给定一个链表，返回链表开始入环的第一个节点。如果链表无环，则返回 null。

一个非常直观的思路是：我们遍历链表中的每个节点，并将它记录下来；一旦遇到了此前遍历过的节点，就可以判定链表中存在环。借助哈希表可以很方便地实现。另外一种思路使用快慢指针：fast 与 slow。它们起始都位于链表的头部。随后，slow 指针每次向后移动一个位置，而 fast 指针向后移动两个位置。如果链表中存在环，则 fast 指针最终将再次与 slow 指针在环中相遇。如下图所示，设链表中环外部分的长度为 $a$，slow 指针进入环后，又走了 $b$ 的距离与 fast 相遇，距离环的起点为 $c$。此时，fast 指针已经走完了环的 $n$ 圈，因此它走过的总距离为 $a+n(b+c)+b=a+(n+1)b+nc$。根据题意，任意时刻，fast 指针走过的距离都为 slow 指针的 2 倍。因此，我们有 $a+(n+1)b+nc=2(a+b)a=c+(n−1)(b+c)$有了 $a=c+(n−1)(b+c)$ 的等量关系，我们会发现：从相遇点到入环点的距离加上 n−1 圈的环长，恰好等于从链表头部到入环点的距离。因此，当发现 slow 与 fast 相遇时，我们再额外使用一个指针 ptr。起始，它指向链表头部；随后，它和 slow 每次向后移动一个位置。最终，它们会在入环点相遇。

ListNode *detectCycle(ListNode *head) {
    ListNode *slow = head, *fast = head;
    while (fast != nullptr) {
        slow = slow->next;
        if (fast->next == nullptr) {
            return nullptr;
        }
        fast = fast->next->next;
        if (fast == slow) {
            ListNode *ptr = head;
            while (ptr != slow) {
                ptr = ptr->next;
                slow = slow->next;
            }
            return ptr;
        }
    }
    return nullptr;
}

数据结构与算法