Leetcode记录：二叉搜索树

15 Aug 2024

二叉搜索树是一个有序树：

若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
它的左、右子树也分别为二叉搜素树

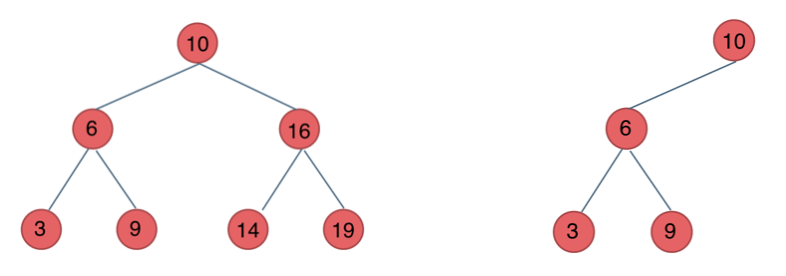
根据二叉搜索树的性质，左节点的值 < 根节点的值 < 右节点的值，我们很容易想到，对二叉搜索树进行中序遍历就可以得到一个节点值递增的序列。因此我们也将二叉搜索树称为二叉排序树。

二叉搜索树的搜索操作

// 递归
TreeNode *searchBST(TreeNode *root, int val) {
    if (root == nullptr) {
        return nullptr;
    }
    if (val == root->val) {
        return root;
    }
    return searchBST(val < root->val ? root->left : root->right, val);
}
// 迭代
TreeNode* searchBST(TreeNode* root, int val) {
    while (root != NULL) {
        if (root->val > val) root = root->left;
        else if (root->val < val) root = root->right;
        else return root;
    }
    return NULL;
}

插入操作

// 递归
TreeNode* insertIntoBST(TreeNode* root, int val) {
    if (root == NULL) {
        TreeNode* node = new TreeNode(val);
        return node;
    }
    if (root->val > val) root->left = insertIntoBST(root->left, val);
    if (root->val < val) root->right = insertIntoBST(root->right, val);
    return root;
}

关于迭代实现方法，在遍历的过程中需要记录一下当前遍历的节点的父节点，这样才能做插入节点的操作：这也是个小技巧：

TreeNode* insertIntoBST(TreeNode* root, int val) {
    if (root == NULL) {
        TreeNode* node = new TreeNode(val);
        return node;
    }
    TreeNode* cur = root;
    TreeNode* parent = root; // 这个很重要，需要记录上一个节点，否则无法赋值新节点
    while (cur != NULL) {
        parent = cur;
        if (cur->val > val) cur = cur->left;
        else cur = cur->right;
    }
    TreeNode* node = new TreeNode(val);
    if (val < parent->val) 
        parent->left = node;// 此时是用parent节点的进行赋值
    else 
        parent->right = node;
    return root;
}

删除操作

 TreeNode* deleteNode(TreeNode* root, int key) {
    if (root == nullptr) return root; // 第一种情况：没找到删除的节点，遍历到空节点直接返回了
    if (root->val == key) {
        // 第二种情况：左右孩子都为空（叶子节点），直接删除节点， 返回NULL为根节点
        if (root->left == nullptr && root->right == nullptr) {
            ///! 内存释放
            delete root;
            return nullptr;
        }
        // 第三种情况：其左孩子为空，右孩子不为空，删除节点，右孩子补位 ，返回右孩子为根节点
        else if (root->left == nullptr) {
            auto retNode = root->right;
            ///! 内存释放
            delete root;
            return retNode;
        }
        // 第四种情况：其右孩子为空，左孩子不为空，删除节点，左孩子补位，返回左孩子为根节点
        else if (root->right == nullptr) {
            auto retNode = root->left;
            ///! 内存释放
            delete root;
            return retNode;
        }
        // 第五种情况：左右孩子节点都不为空，则将删除节点的左子树放到删除节点的右子树的最左面节点的左孩子的位置
        // 并返回删除节点右孩子为新的根节点。
        else {
            TreeNode* cur = root->right; // 找右子树最左面的节点
            while(cur->left != nullptr) {
                cur = cur->left;
            }
            cur->left = root->left; // 把要删除的节点（root）左子树放在cur的左孩子的位置
            TreeNode* tmp = root;   // 把root节点保存一下，下面来删除
            root = root->right;     // 返回旧root的右孩子作为新root
            delete tmp;             // 释放节点内存（这里不写也可以，但C++最好手动释放一下吧）
            return root;
        }
    }
    if (root->val > key) root->left = deleteNode(root->left, key);
    if (root->val < key) root->right = deleteNode(root->right, key);
    return root;
}

二叉搜索树「中序遍历」得到的值构成的序列一定是升序的

验证BST

Leetcode 98. 给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

bool isValidBST(TreeNode* root) {
    stack<TreeNode*> stack;
    long long inorder = (long long)INT_MIN - 1;

    while (!stack.empty() || root != nullptr) {
        while (root != nullptr) {
            stack.push(root);
            root = root -> left;
        }
        root = stack.top();
        stack.pop();
        // 如果中序遍历得到的节点的值小于等于前一个 inorder，说明不是二叉搜索树
        if (root -> val <= inorder) {
            return false;
        }
        inorder = root -> val;
        root = root -> right;
    }
    return true;
}

递归写法，可以避免存在longlong最小值的节点导致无法判断：

TreeNode* pre = NULL; // 用来记录前一个节点
bool isValidBST(TreeNode* root) {
    if (root == NULL) 
        return true;
    bool left = isValidBST(root->left);

    if (pre != NULL && pre->val >= root->val) 
        return false;
    pre = root; // 记录前一个节点

    bool right = isValidBST(root->right);
    return left && right;
}

将二叉搜索树转换一个双向链表

直接中序遍历，前的right指向后，后的left指向前即可。

BST中的最小绝对差

Leetcode 530. 给你一个二叉搜索树的根节点 root ，返回树中任意两不同节点值之间的最小差值。差值是一个正数，其数值等于两值之差的绝对值。

递归版本和迭代版本的中序遍历都可以：

void dfs(TreeNode* root, int& pre, int& ans) {
    if (root == nullptr) {
        return;
    }
    dfs(root->left, pre, ans);
    if (pre == -1) {
        pre = root->val;
    } else {
        ans = min(ans, root->val - pre);
        pre = root->val;
    }
    dfs(root->right, pre, ans);
}
int getMinimumDifference(TreeNode* root) {
    int ans = INT_MAX, pre = -1;
    dfs(root, pre, ans);
    return ans;
}

BST中的众数

Leetcode 501. 给你一个含重复值的二叉搜索树（BST）的根节点 root ，找出并返回 BST 中的所有众数（即，出现频率最高的元素。

如果是二叉树的话就要遍历存入map，再进行排序：

void searchBST(TreeNode* cur, unordered_map<int, int>& map) { // 前序遍历
    if (cur == NULL) return ;
    map[cur->val]++; // 统计元素频率
    searchBST(cur->left, map);
    searchBST(cur->right, map);
    return ;
}
bool static cmp (const pair<int, int>& a, const pair<int, int>& b) {
    return a.second > b.second;
}
vector<int> findMode(TreeNode* root) {
    unordered_map<int, int> map; // key:元素，value:出现频率
    vector<int> result;
    if (root == NULL) return result;
    searchBST(root, map);
    vector<pair<int, int>> vec(map.begin(), map.end());
    sort(vec.begin(), vec.end(), cmp); // 给频率排个序
    result.push_back(vec[0].first);
    for (int i = 1; i < vec.size(); i++) {
        // 取最高的放到result数组中
        if (vec[i].second == vec[0].second) result.push_back(vec[i].first);
        else break;
    }
    return result;
}

但题目中是BST，因此，同样的思路就是使用中序遍历，递归和迭代方法都可以：

vector<int> findMode(TreeNode* root) {
    stack<TreeNode*> st;
    TreeNode* cur = root;
    TreeNode* pre = NULL;
    int maxCount = 0; // 最大频率
    int count = 0; // 统计频率
    vector<int> result;
    while (cur != NULL || !st.empty()) {
        if (cur != NULL) { // 指针来访问节点，访问到最底层
            st.push(cur); // 将访问的节点放进栈
            cur = cur->left;                // 左
        } else {
            cur = st.top();
            st.pop();                       // 中
            if (pre == NULL) { // 第一个节点
                count = 1;
            } else if (pre->val == cur->val) { // 与前一个节点数值相同
                count++;
            } else { // 与前一个节点数值不同
                count = 1;
            }
            if (count == maxCount) { // 如果和最大值相同，放进result中
                result.push_back(cur->val);
            }

            if (count > maxCount) { // 如果计数大于最大值频率
                maxCount = count;   // 更新最大频率
                result.clear();     // 很关键的一步，不要忘记清空result，之前result里的元素都失效了
                result.push_back(cur->val);
            }
            pre = cur;
            cur = cur->right;               // 右
        }
    }
    return result;
}

二叉树/二叉搜索树的最近公共祖先

Leetcode 235/236. 给定一个二叉树/BST, 找到该树中两个指定节点p、q的最近公共祖先。

对于二叉树，如果左子树出现p，右子树出现q，则它就是最近的公共祖先：

TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
    if(root == nullptr) return nullptr;
    if(root->val == p->val || root->val == q->val){
        return root;
    }
    TreeNode *left = lowestCommonAncestor(root->left,p,q);
    TreeNode *right = lowestCommonAncestor(root->right,p,q);
    if(left && right)
        return root;
    if(left==nullptr)
        return right;
    if(right ==nullptr)
        return left;
    return nullptr;
}

如果是二叉搜索树会方便一些：

TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
    TreeNode* ancestor = root;
    while (true) {
        if (p->val < ancestor->val && q->val < ancestor->val) {
            ancestor = ancestor->left;
        }
        else if (p->val > ancestor->val && q->val > ancestor->val) {
            ancestor = ancestor->right;
        }
        else {
            break;
        }
    }
    return ancestor;
}

修剪BST

Leetcode 669. 给你二叉搜索树的根节点 root ，同时给定最小边界low 和最大边界 high。通过修剪二叉搜索树，使得所有节点的值在[low, high]中。

TreeNode* trimBST(TreeNode* root, int low, int high) {
    if (root == nullptr) return nullptr;
    if (root->val < low) return trimBST(root->right, low, high);
    if (root->val > high) return trimBST(root->left, low, high);
    root->left = trimBST(root->left, low, high);
    root->right = trimBST(root->right, low, high);
    return root;
}

把BST转化为累加树

Leetcode 538. 给出二叉搜索树的根节点，该树的节点值各不相同，请你将其转换为累加树（Greater Sum Tree），使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。

本质上就是逆前序遍历：

int sum = 0;
TreeNode* convertBST(TreeNode* root) {
    if (root != nullptr) {
        convertBST(root->right);
        sum += root->val;
        root->val = sum;
        convertBST(root->left);
    }
    return root;
}

有序数组转化为AVLTree

Leetcode 108. 给你一个整数数组 nums ，其中元素已经按升序排列，请你将其转换为一棵平衡二叉搜索树。

每次都从中间分割即可，注意涉及到left和right的边界时刻！

TreeNode* traversal(vector<int>& nums, int left, int right) {
    if (left > right) return nullptr;
    int mid = left + ((right - left) / 2);
    TreeNode* root = new TreeNode(nums[mid]);
    root->left = traversal(nums, left, mid - 1);
    root->right = traversal(nums, mid + 1, right);
    return root;
}
TreeNode* sortedArrayToBST(vector<int>& nums) {
    TreeNode* root = traversal(nums, 0, nums.size() - 1);
    return root;
}

数据结构与算法