绿皮书第二章：Brain Teasers

问题简化

海盗分金

五名海盗抢劫了一个装满 100 枚金币的箱子。 作为一群民主海盗，他们同意以下分配战利品的方法：最资深的海盗将提议分配硬币。 所有海盗，包括最资深的海盗，都将投票。如果至少 50% 的海盗（在这种情况下为 3 名海盗）接受该提议，则按提议分配金币。 如果没有，最高级的海盗将被喂给鲨鱼，这个过程从下一个最高级的海盗开始。重复这个过程，直到计划被批准。 你可以假设所有的海盗都是完全理性的：他们想先活下去，然后尽可能多地获得金币。 最后，作为嗜血的海盗，如果可以选择的话，就算自己获得的金币是一样的，他们希望船上的海盗数量越少越好。

金币最终会如何分配？

1. 1个海盗不用分，都是自己的；
2. 2个海盗也不用分，资深的（第1个）那个肯定全分给自己，因为自己占50%的投票，所以分法是（Remaining，0）；
3. 3个海盗时，最资深的（第1个）知道2个海盗时，第3个海盗会一枚也得不到，因此会给他一枚，而第2个海盗就别想得到了，因为第1个海盗的策略已经得到2/3人的支持，因此分法是（Remaining，0,1）；
4. 4个海盗时，最资深的（第1个）知道3个海盗时，第3个海盗会一枚也得不到，因此给他一枚获得他的投票，其他两个海盗不给，投票50%也能通过，因此分法是（Remaining，0,1,0）
5. 如此动态推下去，分法是（Remaining，0，1,0,1，…, x） 如果海盗数为偶数，x 为0；否则x为1。

老虎和羊

100只老虎和1只羊被放在一个只有草的魔法岛上。 老虎可以吃草，但他们宁愿吃羊。 假设： A. 每次只有一只老虎可以吃一只羊，而那只老虎在吃完羊后自己也会变成一只羊。 B. 所有的老虎都很聪明，完全理性，它们都想活着。 那么羊会被吃掉吗？

1. 1只老虎，羊肯定被吃，因为老虎吃完羊后变成羊，依然可以活着，没有其他老虎会吃他；
2. 2只老虎，羊不被吃，因为先吃羊的那只老虎会被后面一直老虎吃掉，所以哪一只都不会先吃羊，达成一个平衡；
3. 3只老虎，羊被吃，先想出两只老虎情况下羊会不被吃的那只老虎，会吃了羊变成羊，然后活下去；
4. 4只老虎，羊不被吃，因为剩下3只老虎会吃掉变成羊的那只老虎，所以没有老虎会去吃羊，达成平衡；
5. 如此类推，偶数只老虎时，羊不被吃，而奇数只老虎时，羊会被吃。 回到本题，100只老虎，则羊不会被吃。

逻辑推理

快速过河

A、B、C、D 四个人需要过河。 过河的唯一方法是通过一座旧桥，一次最多可容纳 2 人。 天黑了，他们没有手电筒就不能过桥，而他们只有一个手电筒。 所以每一对只能以较慢的人的速度行走。 他们需要尽快将所有这些人带到另一边。 A是最慢的，需要10分钟才能通过； B 需要 5 分钟； C 需要 2 分钟； D 需要 1 分钟。

那么过河最短的时间是多少，方案是什么？

1. 第一趟，让C、D通过，然后C或者D一个人，返回送手电筒；假设为D，则时间为 2 + 1；
2. 第二趟，让A、B通过，然后C或者D剩下的那个人返回送手电，按第一趟的假设，这次应该是C，则时间为10+2；
3. 第三趟，C、D通过，用时2分钟。 此时，全部人都到对岸，总用时3+12+2 = 17分钟。

猜生日

您和您的同事都知道您的老板 A 的生日是以下 10 个日期之一： 3 月 4 日、3 月 5 日、3 月 8 日 6 月 4 日，6 月 7 日 9 月 1 日，9 月 5 日 12 月 1 日、12 月 2 日、12 月 8 日

A 只告诉了你他生日的月份，并告诉了你的同事 C 生日的号数。 之后，你先说：“我不知道A的生日，C也不知道。” 听完你的话，C回答说：“我不知道A的生日，现在我知道了。” 你笑着说：“现在我也知道了。” 在查看了 10 个日期并听取了您的意见后，您的行政助理没有问任何问题就记下了 A 的生日。 那么助理写了什么？

1. “C也不知道”，说明我所知道的月份里，对应的号数都是重复的，这样6月和12月被排除，因为如果C拿到7日或者2日，那就很容易知道生日是哪天。所以现在剩下3月和9月。
2. C已经推理到月份只有3月和9月，那么C能推出生日，说明肯定不是5号，这样 3月5日和9月5日被排除。
3. “现在我也知道了。”这句判断的前提是知道3月5日和9月5日被排除，还剩3月两天，和9月一天。如果你拿到的是3月，肯定没有信心判断是哪天，那么唯一的可能是你拿到的是9月，所以生日是9月1号。

花色牌

赌场提供使用一副普通 52 张牌的纸牌游戏。 规则是你每次翻两张牌。对于每一对，如果两者都是黑色的，则进入庄家的牌堆； 如果两者都是红色的，它们会进入你的堆； 如果一黑一红，则丢弃。 重复该过程，直到你们两个通过所有 52 张卡。 如果您的牌堆中有更多牌，您将赢得 100 美元； 否则（包括牌数相同的情况）你什么也得不到。 赌场允许您协商要为游戏支付的价格。 你愿意花多少钱来玩这个游戏？

一毛钱都不给。因为不管怎么发牌，最终牌数都是相同的。

烧绳计时

你有两根绳子，每根绳子都可以燃烧一个小时。 但是任何一根绳子密度不均，密的地方烧的慢，疏的地方烧的快，不能保证绳子不同段燃烧速度的一致性。 你如何用这两条绳子测量 45 分钟？

首先点燃一根的两头和另一根的一头，开始计时。当两头烧的烧完了，计时半小时，同时点燃另一个绳子的另一头，让它也两头烧，重新计时，当它烧完时，计时15分钟。两个加起来就是45分钟。

用天平区分次品球

有12个球，其中有一个球是次品，跟其他球的重量不一样，是更重还是更轻不清楚。现有一个天平，请问用3次天平测量，如何测出次品球来，并区分是重还是轻。

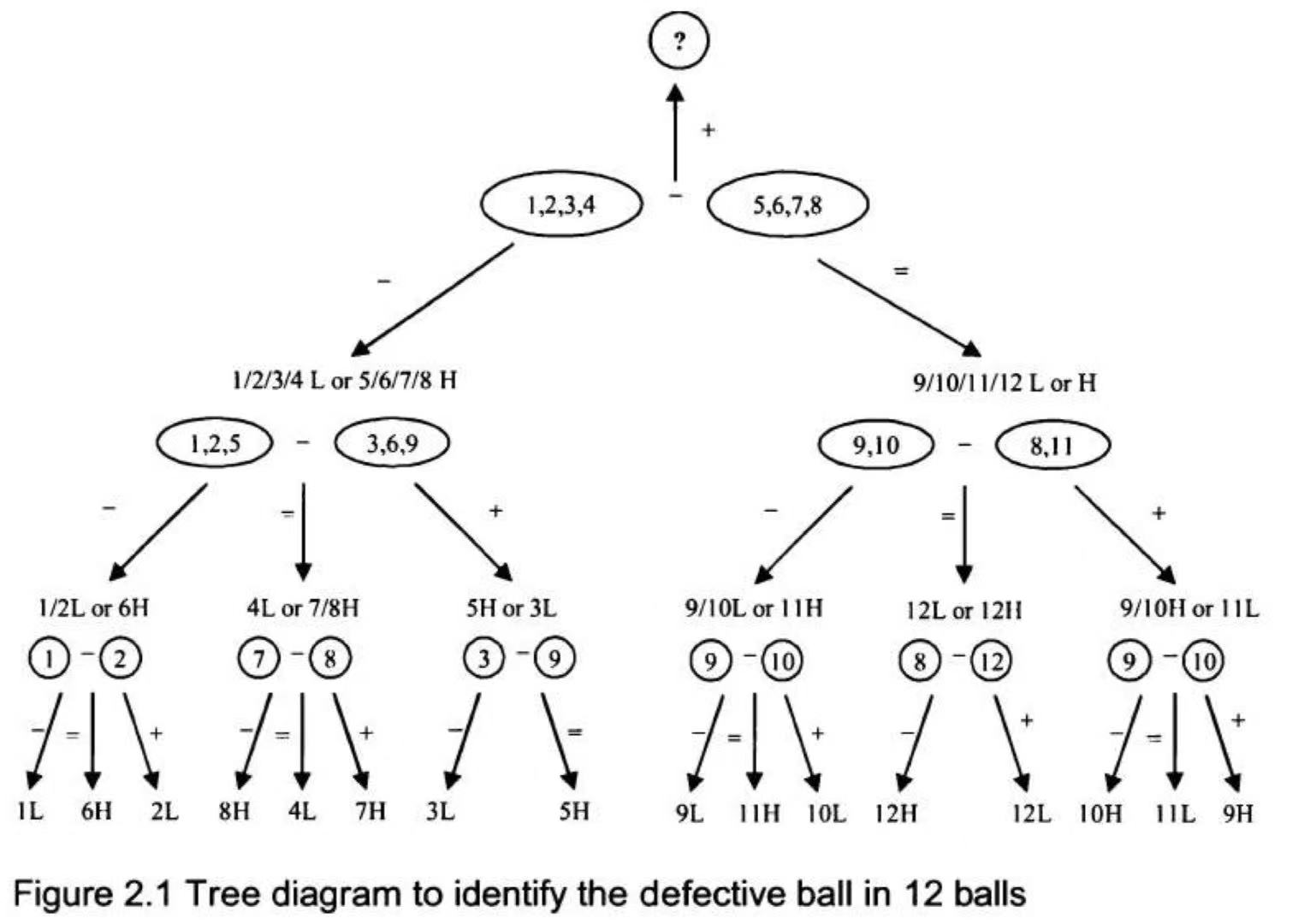
这里面有规律，如果球的缺陷类别（重或轻）已知，则可以用M次测量区分3^M个球中的一个次品球；如果缺陷类别未知，则可以区分(3^M-3)/2个球中的一个次品球。

阶乘尾0的个数

100！的尾部有几个0？

1. 分析相乘产生0 的情况。25 = 10； 425 = 100 =455。 也就是一个5乘一个偶数就能得到1个0，偶数比5的个数要多得多，所以0的个数，取决于能分解出多少个5。那么（5,10，…,100）能分解出多少个5？

2. （5,10,…，100）除以5，有（1,2，…，20），含20个5，另外（1,2，…，20）中还有4个5，因为（5,10,15,20），除以5有（1,2,3,4），没5了，所以总共含有24个5，也就是有24个0。

3. 那么1000！呢？ [5,1000]

   200 + [5,200]

   40 + [5,40]

   8 + [5,8]

   1 = 249个

无限序列

$x^{x^{\cdots}} = 2$，求 x

解答：无限序列的情况，用迭代的思想列方程，$x^{x^{\cdots}} = x^{x^{x^{\cdots}}} = x^2 = 2 \Rightarrow x = \sqrt{2}.$

赛马比赛

有25匹马，一次比赛只能跑五匹马，问最少用多少次比赛可以找到前三个最快的。

1. 先分五组跑五次，设1，6，11，16，21为各组第一；
2. 他们五个再跑一次，假设排名就是1，6，11，16，21；
3. 1肯定是最快的，再让2，3，6，7，11跑一次就可以了。

跳出思维框架

打包箱子

请问能否把53块1x1x4的砖块放到6x6x6的箱子里？

这题是国际象棋题的升级版。国际象棋的题目是二维的，而箱子是三维的，更难一些，但是解法都是一样的。从国际象棋题展开来说。如图象棋棋盘是黑白相间的64个小方格，假设都为1x1，现在拿去对角线上的两个小方块，请问，还能否放入31个1x2的方格进去？

管怎么放1x2的方格，都会占据1黑1白两个方格。那么最多能放几个1x2方格，取决于黑格或者白格的数量最少的那个。本来64个，黑白各32个，但是移除对角线的两个方格，是同颜色的，那么就还剩下30个黑32个白，或者30个白32个黑，所以不论什么情况，最多是30个，占据的面积是60，有两个不相连的方格剩下。

按照这个套路，解决箱子问题。用小正方体给它上色，也就是2x2x2的小箱子。这样的小箱子总共有3x3x3=27个，然后他们颜色相间的话，只能是13黑14白或者13白14黑。同时因为两个黑白的小箱子能装4块砖（底面积是4倍），所以总共能装的是13x4 等于52块砖。注定有一块2x2x2的小箱子浪费。

日历骰子

用2个自制的骰子（6面），刻画所有月份里的天数，仅仅是天数。其中第一天为01，一个骰子显示0，一个显示1。那么请问该如何设计这两个骰子。

1. 012345
2. 012678
3. 6和9是对称的，只要刻一个数字就可以表达2个数

offer之门

假如两个守卫守着两扇门，一扇通往offer，一扇“谢谢你的投递，but you failed”。两守卫一个诚实只说真话，一个狡猾只说假话。你只能问其中一个守卫一句只能用yes/or回答的问题，你如何问，才能顺利打开offer之门？

问其中一个守卫“另一个守卫会说你守的是offer门吗？”，如果该守卫说是的，则选另一扇门，如果说No，那就是这扇门。

挂锁快递

你想给上海的朋友发快递送物资，但是最近时局动荡，没上锁的快递不安全，东西会丢，需要用挂锁箱子运送。但是目前你跟你朋友各自有一把锁，但是各自都只有一把钥匙，那么应该怎么送，物资才能安全送达？

第一趟送的时候挂你的锁，安全送到上海，但是你朋友打不开。没关系，你朋友在箱子上又挂了一把他自己的锁，然后快递送回来，你把自己的锁解开，再快递到上海，这时候，就是你朋友的锁在保护物资了。平安到上海后，你朋友就可以打开箱子获得物资了。

最后一球的颜色

如果袋子里有20个蓝球，14个红球。每次抽两个球，不放回，扔掉。如果抽出的是同色的，往袋子里添加一个蓝球；如果是不同色的，则添加一个红球。假设球足够进行这些操作。请问，袋子里最后一个球是什么颜色的？如果是20个蓝球，13个红球呢？

观察各个组合带来的蓝球和红球的变动规律，蓝球奇数变动，要么加1要么减1；红球要么不变，要么减2，都是偶数变动。所以如果14个红球的话，最后肯定变成0，13个红球的话最后肯定变成1。

控制灯的开关是哪个

屋外有四个开关，屋内有一盏灯，其中只有一个开关控制灯。你在屋外不能及时看到灯的状态。请问至少需要进屋几次才能分辨出控制灯的开关是哪个，该如何操作。

灯除了明灭的信息，还有冷热的信息，那么两种状态（亮否，热否）可以表示四种可能情况。那么我们可以先闭合1和2开关，等待一段时间。然后把开关2断开，合上开关3，立即进屋查看灯的两种状态。判断规则如下：

1. 如果灯是亮且热的，那么开关1控制；
2. 如果灯是亮但不热的，那么开关3控制；
3. 如果灯是暗但热的，那么开关2控制；
4. 如果等是暗且不热的，那么开关4控制。

求量化平均工资

5个量化工程师去酒吧喝酒，他们好奇量化行业的平均工资是多少，但是又不想暴露自己的收入情况。请问有什么方法可以在不暴露各自收入的情况下，求得他们的收入均值？

第一个工程师设置一个随机初值，写上自己的收入与初值的加和，然后传递给第二个工程师；第二个工程师也加上自己的收入，依次加总完后，将数据给第一个工程师，他将最后的总数减去随机初值，然后除以人数，就是他们收入的均值。这里并没有泄露任何人的真实收入。

巧用对称性

确保两堆硬币有同样数量的字面朝上

假设有1000个硬币，其中有20个字面朝上，980个花面朝上；你不能通过触摸感受硬币是哪一面，但是你可以无限次数的翻转硬币。请问怎么分，才能确保分出来的两堆硬币字面朝上的硬币数量相同？

假设给第一堆分了n个硬币，其中有m个字面朝上的，那么另一堆则有1000-n个硬币，其中20-m个字面朝上。我们要确保两边的字面朝上，且手段只有翻面。那么

从1000个硬币中随机选20个，不管这20个里面是否有字面朝上的硬币，都给翻转过来，就能保证这两堆里，字面朝上的硬币数量相等。

打错标签的水果袋

有三袋水果，分别装着梨、苹果以及苹果和梨的混装。每个袋子外面打了相应的标签，但是现在水果店老板告诉你，标签都打错了，你可以拿出水果来判断袋子的正确标签，那么请问怎么拿最少次数水果，更正所有的标签？你可以拿无数次，袋子是非透明的。

1. 一次即可，从标记为混装的袋子里拿水果，拿出来的是梨，那么这个袋子里装的就全是梨；拿出来的是苹果，那么这个袋子里装的就全是苹果。它不会出现混装的情况，因为题目告诉了，所有标签都错了。
2. 假设我们从混装袋子里拿出的是梨，那么标签为梨的袋子里装的肯定是苹果，标签为苹果的就是混装。

智者斗酋长

野人酋长抓了50个智者。每分钟他随机抓一个智者去问话，问话前每个智者可以翻转大堂门口的一个玻璃杯，也可以不翻转。如果智者可以肯定地正确地回答“所有智者至少被酋长问过一次话”，那么酋长会放了所有人。否则，回答错误的话，也就是说不是所有人都被问过话，但有智者回答是，那么所有人会被献祭。在他们被关到各自牢房（一人一间）前，他们可以聚集一次商量对策。 那么智者该如何应对才能活下来。被问话的智者是随机且无限次抽取的。不回答不视为答错，智者在没把握的时候可以选择不回答。

1. 非破题人初次被喊话：
   1. 如果杯子是正放的，倒置它（发出信号，等待破题人接收）
   2. 如果杯子是倒置的，不操作；（另一个人发出的信号，且未被破题人归置，也就是信号还未传达至破题人）
2. 非破题人非初次被喊话：
   1. 如果自己未翻转过杯子且杯子是正放的，倒置它；（发出自己的信号，等到接收）
   2. 如果自己已经翻转过杯子，则不做任何操作；
3. 破题人：
   1. 如果杯子是倒置的，计数+1，然后摆正杯子；（接收到信号，1人至少被问话一次）
   2. 如果杯子是正放的，不做操作。这样计数到49时，就可以答题了。

数列求和

钟表碎片

一块钟表刻度为1,2，…，12，摔碎成了连续的3块，且每块的刻度数字和相同，请问碎成了哪三块？

第一块肯定是11,12,1,2；那么往两边推，11点前面的是10,9，加8就超过26了，然后2点往后是3,4, 所以第二块是9,10,3,4；剩下的为第三块，7,8,5,6。

缺失的整数

1到100个整数里，缺了两个，问怎么快速得到这个缺失值？

分别求一次和和二次和，列两个方程，然后解方程。

快速定位劣币袋子

有10袋子硬币，每袋100个硬币，每个真币重10克。其中有一袋的硬币全是假币，可能比真硬币重1克，也可能轻1克（全都重或者全都轻）。现在有个电子秤，请问如何用最少的次数称重，找出假币的袋子？

第一个袋子拿1个硬币，第二个袋子拿2个硬币，如此类推，第10个袋子拿10个硬币，这样假硬币的数量就能反向指出袋子的编号。

类似的还有用二进制序列来区分试剂药品之类的题。比如有1000罐药，其中有一罐有毒，一点就致命，但是需要一天才能显现效果，现在有10只小白鼠，问该如何测试，才能最快把毒药辨别出来？方法是混合试剂，用2进制的方式混。如第9罐药，对应10位的2进制为“0000001001”，也就是喂第7只和第10只小白鼠喝第9罐药（一丁点）。如此类推，将药罐的编号变换为对应的10位2进制，然后为1的数对应的小白鼠喝药，最后看小白鼠的死亡pattern，转换成对应的二进制数，再换算成药罐的序号，就可以在一天内找到毒药。

不管是连续序列，还是2进制变换，本质是要找到一种传递信息或者区分的方式。

100楼层测试玻璃球硬度

假设你有两颗玻璃球，楼有100层，采用楼层高度表述玻璃球的硬度。当球从小于X层往下掉时不会碎，而当从大于等于X层处下落时会碎。那么考虑最坏的情况，应该怎么测试才能最小化球下落的次数，从而测试出玻璃球的硬度。

假设最坏情况，我们至少要扔N次玻璃球。第一球从N层下落，如果碎了，第二个球从1层开始测到N-1层，肯定能测出X；如果第一球层N层下落，没碎，那么下一步，需要从第N+N-1层下落进行测试，因为如果碎了，另一球可以从N+1层测试到2N -2层，测试N-2次；如此类推，第一球如果没碎，则每次间隔减少1层，直到在N次测试时，覆盖100层楼，也就是 N+（N-1）+(N-2)+… + 1 >=100, 求得N>=14，取最小值14，也就是最少扔14次，不论怎么样，可以测出球的硬度。

鸽笼原理

n只鸽笼，mn+1只鸽子，分配到各个鸽笼里，至少有一只笼子里的鸽子不小于m+1只，也就是至少有m+1只鸽子要共享一只笼子。

袜子成对

假设你有黄绿红三色袜子x, y, z只（x，y，z均大于0，x+y+z>3），请问随机取，取多少次一定能配上一对？

4次。

是否有两人握手次数相同

假如你是新上任的领导，第一次去见你的n个团队成员，他们列成一排一一跟你握手。同时他们之间也有新来的相互不认识也会互相握手打招呼。那么请问你是否能肯定地说，“这些人中，至少有两人握手的次数是相同的”。

n+1个人，每个人握手1到n次，因此一定至少有两人握手的次数是相同的。

我们之前见过吗

晚会上有6人，证明要么至少3人是熟人，要么至少3人是陌生人。

首先，假设我是第六个人，至少有三个人见过我或者没见过我。

1. 如果有三个人见过我：如果有两个互相见过，那加上我就是三个；否则他们三个是陌生人。
2. 如果有三个人没见过我：如果有两个是陌生人，加上我就是三个；否则他们三个是熟人。

正方形中的蚂蚁

一个边长为1的正方形中有51个蚂蚁，你有一个1/7半径的瓶子，是否能找到一个地方放瓶子能盖住至少三个蚂蚁？

可以的。首先将正方形分为5x5个小正方形，肯定有一个上至少有三个蚂蚁。同时 $1/5 < \sqrt{2}/7$说明瓶子能盖住这个小正方形。

找假币II

现在有五个袋子，每个里面有100个硬币，每个袋子中的硬币都是相同的，但是有可能是9g、10g或者11g。我们不知道每个袋子里装的是哪种硬币，你需要几次测量来得到每个袋子中的硬币种类？

1. 如果只有两个袋子的话，此时解空间有9种可能，那么我们就需要第一个袋子取1个，第二个袋子取3个，这样总和在-4到4中间，正好是9个情况：
   
2. 三个袋子的话，有27个可能，第三个袋子就需要取9个。
3. 以此类推，我们需要从每个袋子中依次取1,3,9,27,81个来测量就可以了。

取余运算

猜帽子颜色

有100个犯人，每个人会给一个红色或者蓝色帽子，他们可以看到别人的帽子但看不到自己的，每个人都会被随机叫去猜自己帽子颜色，猜对了就放走，请问最多能让多少犯人活下来？

可以至少让99个活下来，第一个犯人如果看到红色帽子个数为奇数就说自己是红色的，否则说自己是蓝色的。这样其他人都能推断出自己帽子是什么颜色的。

三个颜色也是一样的道理。

被9整除

给定一个整数，证明为什么各个位数相加能被9整除，原数就能被9整除。

$a=a_n10^n+\cdots+a_1 10^1 + a_0, a_n+\cdots+a_0 = 9x \Rightarrow b = a_n(10^n-1)+\cdots+a_1(10^1-1) = a - 9x$ b是可以被9整除的，因此a可以被9整除。

同理可证$(-1)^na_n+\cdots+(-1)a_1+a_0$ 被 11 整除 当且仅当 a 可以被11整除。

变色龙颜色

岛屿上有13个红色变色龙，15个绿色和17个蓝色，每当两只不同颜色的变色龙相遇时就会变成第三种颜色，请问最后他们会变成同一种颜色吗？

假如(m+1,n+1,p+1)可以变成同一种颜色，那么(m,n,p)也是可以的。因此我们考虑(0,2,4)即可，而(0,2,4)是永远变不到(0,0,6)的。

数学归纳法

硬币分配问题

假如有1000个硬币，分为两堆，分别有x和y个，此时相乘得到xy，再分别将两堆进行划分，此时得到xy+x1x2+y1y2，以此类推直到每堆只有一个硬币，请问最后的和是多少？

证明$f(n)=\frac{n(n-1)}{2}$即可。

巧克力问题

一个6x8的巧克力，需要多少下才能掰成48个小块呢？

证明$f(m,n) = mn-1$即可。

卡车出发点

一个环形路上有N个加油站，每个加油站的油量总和是支撑得住车开一圈的，假设最初车没油，请问如何选取加油站作为出发点才能跑完一圈？

Leetcode的一道贪心问题。 设油为x_1,…,x_N，路程油耗为y_1,…,y_N。从头开始遍历，如果x_1+…+x_m < y_1+…+y_m，就将起点设为m+1，再从m+1重新从0计算油量和油耗。

反证法

证明$\sqrt{2}$是无理数

假设$\sqrt{2} = \frac{a}{b}$并且gcd(a,b)=1，则有$a^2 = 2b^2$，a为偶数且a被4整除，因此b也是偶数，这就出现了矛盾。

彩虹帽

有七个犯人，每个人带彩虹中的一个颜色的帽子，他们能看到别人的帽子但看不到自己的。让他们猜自己帽子的颜色，有一个猜对的就解放，请问是否能够做到。

设七个颜色分别对应0,1,2,3,4,5,6，记每个人的帽子颜色为$x_i$，他们的猜测为$g_i$，那么就让每个人$(g_i+\sum_{k\neq i}x_k) \% 7 = i$

如果$g_i\neq x_i$，那么 $\sum_{i=1}^7 x_i \% 7 \neq i, i=0,1,2,3,4,5,6$，这样就出现了矛盾。

• 量化绿皮书