概率论:随机变量(绿皮书+额外补充)
一元随机变量与分布函数
离散型随机变量
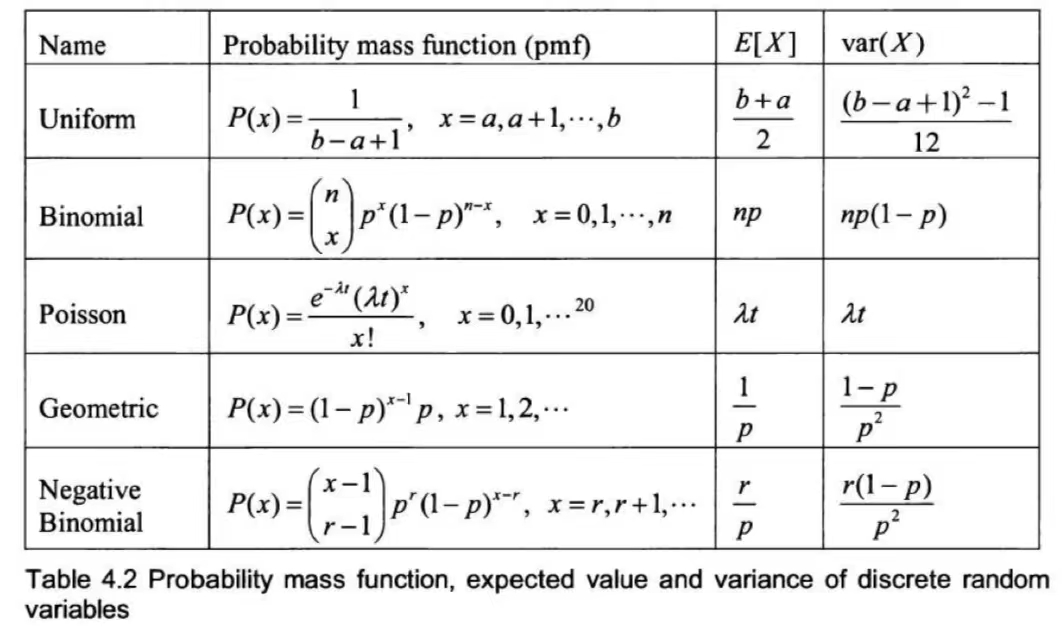
- 0-1分布:$P(X=0)=p,P(X=1)=1-p$.
- 二项分布:X可看做n个0-1分布重复独立试验,试验成功的次数,$P(X=k) = C_n^kp^k(1-p)^{n-k}$,记作$X \sim B(n,p).$
- 泊松分布:$P(X=k) = \frac{e^{-\lambda}\lambda^k}{k!}$,记作$X \sim P(\lambda)$.
- 超几何分布:$P(X=k)=\frac{C_a^kC_b^{n-k}}{C_N^n}$,记作$X\sim H(n,a,N)$,就是N个球,a个红球b个白球,不放回取n个,X为红球的个数。
- 几何分布:$P(X=k)=p(1-p)^{k-1}$,独立重复Bernoulli试验,第k次首次成功的概率。
- 负二项分布:$P(X=k)=C_{k-1}^{r-1}(1-p)^{kr}p^r$,试验进行到出现r次成功才停止,X为饰演的次数。
可以证明当n足够大,p足够小,且np保持适当大小时,$B(n,p)$可以用$P(np)$近似表述。
概率分布函数
概率分布函数定义为$F(x) = P(X\leq x)$,具有以下性质:
- $P(x_1\leq X \leq x_2) = F(x_2) - F(x_1) + P(X=x_1)$
- $F(x)$单调不减
- $0\leq F(x) \leq 1, \lim_{a\rightarrow -\infty}F(a) = 0, \lim_{a\rightarrow \infty}F(a) = 1.$
- $F(x)$右连续,离散型的$F(x)$没有左连续。
连续型随机变量
如果存在一个非负实函数$f(x)$满足$F(x)=\int_{-\infty}^x f(t)dt$,则称X为连续型随机变量,$f(x)$为概率密度函数,具有以下性质:
- $f(x)\geq 0$
- $\int_{-\infty}^{\infty}f(t)dt = 1$
- $\forall x_1<x_2, P(x_1\leq X\leq x_2) = \int_{x_1}^{x_2} f(t)dt$
- 在$f(x)$的连续点处,$F’(x)=f(x)$
- $\forall a, P(X=a) = 0.$
常见的连续型随机变量:
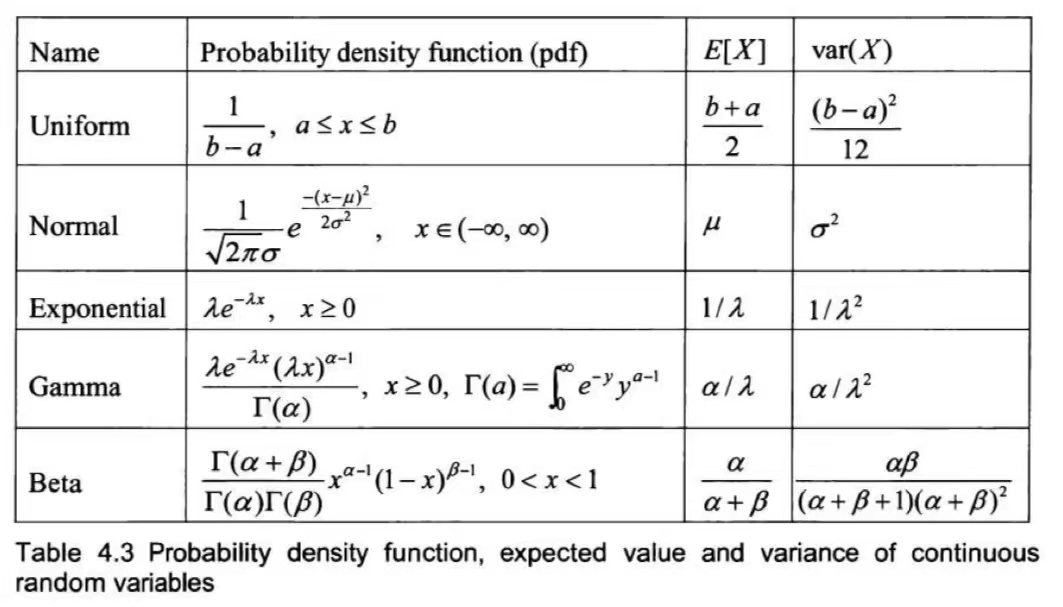
- 均匀分布:$f(x)=\begin{cases}
\frac{1}{b-a}, x\in(a,b)
0, 其他 \end{cases}$,记作$X\sim U(a,b).$ $P(c<X<c+l) = \frac{l}{b-a}, F(x)=\begin{cases} 0, x<a \ \frac{x-a}{b-a}, a\leq x < b
1, x\geq b \end{cases}$ -
指数分布:$f(x)= \begin{cases} \lambda e^{-\lambda x}, x> 0
0, x\leq 0 \end{cases}$,记作$X\sim E(\lambda).$ $F(x) =\int_{-\infty}^x f(t)dt = \begin{cases} 1-e^{-\lambda x}, x>0 \ 0, x\leq 0 \end{cases}$指数分布最重要的性质是无记忆性:$P(X>t_0+t|X>t_0) = \frac{P(X>t_0+t)}{P(X>t_0)} = e^{-\lambda t} = P(X>t)$,即$P(X>t_0+t) = P(X>t_0)P(X>t)$.可以联想到某产品的正常使用时长。 类似的无记忆性还有几何分布:$P(X-m=n)=P(X=m)P(X=n)$,可以联想到抛硬币。
- 正态分布:$f(x)=\frac{1}{\sqrt{2\pi}\sigma}e^{\frac{-(x-\mu)^2}{2\sigma^2}}, |x| < +\infty,\sigma>0,|\mu|<+\infty$,记作$X\sim N(\mu,\sigma^2)$服从参数为$(\mu,\sigma)$的正态分布。
(补充:$\int_{-\infty}^{+\infty}e^{-x^2}dx=\sqrt{\pi}.$)
正态分布具有以下性质:
- $f(x)$关于$x=\mu$对称
- $ \max f(x) = f(\mu) = \frac{1}{\sqrt{2\pi}\sigma}$
- $ \lim_{|x-\mu|\rightarrow \infty} f(x) = 0$
当$\mu=0,\sigma=1$的时候称为标准正态分布,密度函数为$\varphi(x)=\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}$,分布函数为$\varPhi(x) = \int_{-\infty}^x \frac{1}{\sqrt{2\pi}}e^{-\frac{t^2}{2}}dt$,具有性质:
- $\varPhi(-x) = 1-\varPhi(x)$
- 当$X\sim N(\mu,\sigma^2)$时,$\frac{X-\mu}{\sigma} \sim N(0,1) \Rightarrow P(a<x<b) = \varPhi(\frac{b-\mu}{\sigma})-\varPhi(\frac{a-\mu}{\sigma})$
一维随机变量函数的分布
若X分布已知,Y=g(X).
- 当Y是离散型时,找到${Y=y_k}$的等价事件${X\in D_k}$,则有$P(Y=y_k) = P(X\in D_k)$.
- 当Y是连续型时同样可以求出分布函数$F_Y$,求导获得$f_Y$.
如果$X$为连续型,密度函数为$f_X(x),\ y=g(X)$,如果$y=g(X)$严格单增(减),记$y=g(x)$的反函数为$x=h(y)$,则有
\[f_Y(y) = \begin{cases} f_X(h(y))\|h'(y)\|, y\in D \\ 0, y\notin D \end{cases}, D为y=g(x)的值域.\]1. $X\sim N(\mu,\sigma)$,求$aX+b$的密度函数: $y=g(X)=aX+b \Rightarrow x = h(y) = \frac{y-b}{a}$, $h’(y)=\frac{1}{a} \Rightarrow f_Y(y) = \frac{1}{|a|}f_X(\frac{y-b}{a}).$
2. $X\sim U(0,\pi),Y=\sin(x)$,求$f_Y(y)$:
当$0< y \leq 1, F_Y(y)=P(Y\leq y) = P(X\in[0,\arcsin y]\cup [\pi-\arcsin y,\pi]) = \frac{2\arcsin y}{\pi}$
因此$f_Y(y)=\begin{cases}
\frac{2}{\pi} \frac{1}{\sqrt{1-y^2}}, 0 < y \leq 1
0, 其他
\end{cases}$
(补充:$(\arccos x)’ = -\frac{1}{\sqrt{1-x^2}}, (\arctan x)’ = \frac{1}{1+x^2}.$)
有了连续型随机变量后可以去证明$P(AB)=0$并不能证明AB互斥,比如在$(0,1)$上取值,A为(0,0.5],B为[0.5,1).
多元随机变量及其分布
二元离散型随机变量
- 联合分布律:$P(X=x_i,Y=y_j) = p_{ij}, \sum_{i,j}p_{ij}=1, p_{ij}\geq 0.$
-
边际分布:$p_{i\cdot}=\sum_{j}p_{ij} = P(X=x_i), p_{\cdot j} = \sum_i p_{ij} = P(Y=y_j).$
- 条件分布:$P(X=x_i | Y=y_j) = \frac{p_{ij}}{p_{\cdot j}}$, P(Y=y_j | X=x_i) = \frac{p_{ij}}{p_{i\cdot}}.$
分布函数
- 联合分布函数:$F(x,y) = P(X\leq x, Y \leq y)$,有性质:
- $F(x,y)$单调不减
- $0\leq F(x,y) \leq 1, F(x,-\infty) = F(-\infty,y) = 0, F(+\infty,+\infty) = 1.$
- $F(x,y)$关于x或y右连续
- $P(x_1<X\leq x_2, y_1 < Y \leq y_2) = F(x_2,y_2)- F(x_1,y_2) -F(x_2,y_1)+F(x_1,y_1).$
- 边际分布函数:$F_X(x) = P(X\leq x) = F(x,+\infty), F_Y(y)= F(+\infty,y).
- 条件分布函数:
- 离散型:$F_{Y|X}(y|x_i) = P(Y\leq y| X=x_i)$
- 连续型:$F_{Y|X}(y|x) = \lim_{\delta\rightarrow 0^+} P(Y\leq y| x < X \leq x+\delta)$
连续型随机变量
- $F(x,y) =\int_{-\infty}^x\int_{-\infty}^y f(u,v) dudv$,$f(x,y)$称为联合概率密度函数,性质有:
- $f(x,y)\geq 0$
- $\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty} f(x,y) dxdy = F(+\infty,+\infty) =1$
- 在$f(x,y)$连续点上有$\frac{\partial^2F}{\partial x\partial y} = f(x,y).$
- $P((X,Y)\in D) = \int\int_D f(x,y) dxdy.$
- 边际概率密度函数:$F_X(x) = P(X\leq x) = \int_{-\infty}^x[\int_{-\infty}^{+\infty}f(x,y)dy]dx \Rightarrow f_X(x) = \int_{-\infty}^{\infty}f(x,y)dy.$ 同理 $f_Y(y) = \int_{-\infty}^{+\infty}f(x,y)dx.$
- 条件分布:$F_{Y|X}(y|x) = \lim_{\delta\rightarrow 0^+} P(Y\leq y| x < X \leq x+\delta) = \lim_{\delta\rightarrow 0^+}\frac{F(x+\delta,y)-F(x,y)}{F_X(x+\delta) - F_X(x)} = \int_{-\infty}^y \frac{f(x,v)}{f_X(x)}dv.$
因此条件概率密度函数$f_{Y|X}(y|x)=\frac{f(x,y)}{f_X(x)}.$
二元均匀分布:$f(x,y) = \begin{cases}
\frac{1}{S(D)}, (x,y)\in D
0, 其他 \end{cases}$
二元正态分布:$f(x,y) = \frac{1}{2\pi\sigma_1\sigma_2\sqrt{1-\rho^2}}\exp{-\frac{1}{2(1-\rho^2)}[\frac{(x-\mu_1)^2}{\sigma_1^2} - 2\rho\frac{(x-\mu_1)(y-\mu_2)}{\sigma_1\sigma_2} + \frac{(y-\mu_2)^2}{\sigma_2^2}]}$,有以下性质:
- $X\sim N(\mu_1,\sigma_1^2), Y\sim N(\mu_2,\sigma_2^2).$
- 给定$X=x, Y \sim N(\mu_2+\rho\frac{\sigma_2}{\sigma_1}(x-\mu_1), (1-\rho^2)\sigma_2^2)$
- 给定$Y=y, X \sim N(\mu_1+\rho\frac{\sigma_1}{\sigma_2}(y-\mu_2), (1-\rho^2)\sigma_1^2)$
如果X为离散型随机变量,概率分布为p_X(x_i),由全概率公式有\(P(A)=\sum_iP(A\|X=x_i)P(X=x_i)\) 如果X为连续型,其密度函数为$p_X(x)$,则\(P(A) = \int_{-\infty}^{+\infty}P(A\|X=x)p_X(x).\)
例子:设$U_1,\cdots,U_n$独立同分布于$(0,1]$上的均匀分布,令$\xi = \min{n\geq 1: U_1+\cdots+U_n > 1}$,求$\xi$的概率分布。
令$\xi(x)=\min{n\geq 1: U_1+\cdots+U_n > x}$,则有 $P(\xi(x)> 1) = P(U_1\leq x) = x$,进而有递推关系 \(\begin{align*} P(\xi(x)>n+1) &= P(U_1+\cdots+U_{n+1} \leq x) \\ &= \int_{-\infty}^{+\infty}P(U_1+\cdots+U_{n+1} \leq x \| U_1 = y)p_{U_1}(y)dy \\ &= \int_0^1 P(U_2+\cdots+U_{n+1} \leq x-y)dy \\ &= \int_0^x P(\xi(u)>n)du \end{align*}\) 由归纳法可以得到$P(\xi(x)>n) = \frac{x^n}{n!}$,因此可以得到$P(\xi>n)=\frac{1}{n!}\Rightarrow P(\xi = n) = \frac{1}{(n-1)!} - \frac{1}{n!}.$
随机变量的独立性
离散型:$p_{ij} = p_{i\cdot}p_{\cdot j}, i,j=1,2,\ldots$ 连续型:$f(x,y) = f_X(x)f_Y(y), a.e. \Leftrightarrow f(x,y)$几乎处处可以写为$m(x)$与$n(y)$的乘积,注意f的取值范围,y不能与x有关
例:二元正态分布中,XY相互独立$\Leftrightarrow \rho = 0.$
二元随机变量函数的分布
$Z=X+Y$的分布
离散型:\(P(Z=z_k) = \sum_{i=1}^{\infty}P(X=x_i, Y=z_k-x_i), k=1,2,\ldots.\)
连续型: \(\begin{align*} F_Z(z) &= \int\int_{x+y\leq z} f(x,y)dxdy \ \int_{-\infty}^{+\infty}dx\int_{-\infty}^{z-x} f(x,y)dy \\ &= \int_{-\infty}^z dv \int_{-\infty}^{+\infty} f(u,v-u)du\quad(u=x,v=x+y) \\ f_Z(z) &= \int_{-\infty}^{+\infty} f(x,z-x)dx = \int_{-\infty}^{+\infty}f(z-y,y)dy \end{align*}\) 特别地,当XY相互独立时,\(f_Z(x) = \int_{-\infty}^{+\infty}f_X(x)f_Y(z-x)dx = \int_{-\infty}^{+\infty} f_X(z-y)f_Y(y)dy.\)
例:
- $X,Y$相互独立,$X\sim P(\lambda_1), Y\sim P(\lambda_2) \Rightarrow X+Y \sim P(\lambda_1+\lambda_2)$
- ${X_i}$相互独立,$X_i\sim N(\mu_i,\sigma_i^2) \Rightarrow \sum_iX_i \sim N(\sum_i\mu_i, \sum_i \sigma_i^2).$
$Z=\frac{X}{Y}$的分布
\[\begin{align*} F_Z(z) &= P(\frac{X}{Y}\leq z) = \int\int_{x/y\leq z}f(x,y)dxdy \\ &= \int_0^{\infty}dy\int_{-\infty}^{yz}f(x,y)dx + \int_{-\infty}^0dy\int_{yz}^{+\infty}f(x,y)dx \\ &= \int_{-\infty}^z \left[ \int_0^{\infty}p(ay,y)ydy -\int_{-\infty}^0 p(ay,y)ydy\right]da\quad (这里令x=ay) \\ &= \int_{-\infty}^zp_Z(a)da \\ p_Z(z) &= \int_{-\infty}^{\infty}p(zx,x)\|x\|dx. \end{align*}\]次序统计量的分布
设$X_1,\ldots, X_n$独立同分布,分布函数均为$F(x)$,令$\xi_1 = \min(X_1,\ldots,X_n), \xi_2 = \max(X_1,\ldots,X_n).$
\[\begin{align*} P(\xi_2 \leq x) &= P(X_1\leq x,\ldots, X_n\leq x) \\ &= P(X_1\leq x)\cdots P(X_n\leq x) \\ &= [F(x)]^n \\ p(x) &= nf(x)(F(x))^{n-1} \end{align*}\] \[\begin{align*} P(\xi_1 > x) &= P(X_1 > x, \ldots, X_n > x) \\ &= [1-F(x)]^n \\ P(\xi_1 \leq x) &= 1-[1-F(x)]^n. \\ p(x) &= nf(x)[1-F(x)]^{n-1} \end{align*}\]$(\xi_1,\xi_2)$的联合分布函数 \(\begin{align*} F(x,y) &= P(\xi_1\leq x, \xi_2 \leq y) \\ &= P(\xi_2 \leq y) - P(\xi_1 > x, \xi_2\leq y) \\ &= [F(y)]^n - P(\bigcap_{i=1}^n(x < \xi_i \leq y)) \\ &=\begin{cases} [F(y)]^n - [F(y) - F(x)]^n , x<y \\ [F(y)]^n, x\geq y \end{cases} \end{align*}\)
最大值和最小值的相关系数
$X_1,X_2$独立同分布于$U(0,1), Y=\min(X_1,X_2), Z+\max(X_1,X_2)$,请问给定$Z\leq z$时$Y\geq y$的概率是多少? Y和Z的相关系数是多少?
通过画图可以看出来$P(Y\geq y | Z\leq z) = \begin{cases} (z-y)^2 / z^2, 0\leq y \leq z \leq 1, 0, 其他 \end{cases}$
$\rho_{YZ} = \frac{Cov(Y,Z)}{\sqrt{Var(Y)Var(Z)}}$
首先求$Var(Y),Var(Z),f_Y(x)=2(1-x),f_Z(z)=2z$,可以去计算$E(Y)=\frac{1}{3},E(Z)=\frac{2}{3},E(Y^2)=\frac{1}{6},E(Z^2)=\frac{1}{2}\Rightarrow Var(Y)=E(Y^2)-E(Y)^2 = \frac{1}{18}, Var(Z)=\frac{1}{18}.$
紧接着要计算$E(YZ)=\int_0^1\int_0^zyzf(y,z)dydz$,因此要求$Y,Z$的联合密度函数,先计算联合分布函数: $F(y,z)=P(Y\leq y, Z\leq z) = P(Z\leq z) - P(Y\geq y,Z\leq z) = z^2-(z-y)^2 = 2zy-y^2 \Rightarrow f(y,z) = \frac{\partial F(y,z)}{\partial y\partial z} = 2.$
因此$E(YZ)=\int_0^1 \int_0^z 2yzdydz = \frac{1}{4}\Rightarrow Cov(Y,Z) =E(YZ)-E(Y)E(Z)=\frac{1}{36} \Rightarrow \rho_{YZ}=\frac{1}{2}.$
随机向量的变换
$(\xi_1,\ldots,\xi_n)$密度函数为$p(x_1,\ldots,x_n)$,现有$m$个函数$\eta_i = f_i(\xi_1,\ldots,\xi_n)$,其联合分布函数为\(G(y_1,\ldots,y_m)=P(\eta_1\leq y_1,\ldots, \eta_m\leq y_m) = \int_\cdots\int_D p(x_1,\ldots,x_n) dx_1\cdots dx_n.\) 其中$D ={(x_1,\ldots,x_n : \eta_1\leq y_1,\ldots, \eta_n \leq y_n)}$
如果$m=n$并且$f_i$有唯一反函数组$x_i = x_i(y_1,\ldots,y_n)$并且$J = \frac{\partial(x_1,\ldots,x_n)}{\partial(y_1,\ldots,y_n)}\neq 0$,那么有 \(q(y_1,\ldots,y_n) = \begin{cases} p(x_1(y_1,\ldots,y_n),\ldots)\|J\|, (y_1,\ldots,y_n)\in (\eta_1,\ldots,\eta_n)的值域 \\ 0, 其他 \end{cases}\)
数字特征
数学期望
离散型:$EX=\sum_k x_kp_k$ 连续型:$EX=\int_{-\infty}^{\infty}xp(x)dx$
有以下性质:
- $E(g(X)) = \int g(x)p(x)dx$
- 可加性
- 有限个独立的随机变量乘积的期望等于乘积的期望
条件期望
$E(\eta|\xi =x) = \int_{-\infty}^{\infty} ydF_{\eta|\xi}(y|x)$
离散型:$E(\eta|\xi =x) = \sum_j y_jp_{\eta|\xi}(y_j|x)$ 连续型:$E(\eta|\xi =x) = \int_{-\infty}^{\infty} y p_{\eta|\xi}(y|x)dy$
全期望公式
$E(X) = E(E(X|Y)) = \begin{cases}
\sum_y E(X|Y=y)p(Y=y), Y为离散型
\int_{-\infty}^{\infty} E(X|Y=y)f_Y(y)dy, Y为连续型
\end{cases}$
方差、协方差、相关系数
方差$Var\xi = E(\xi-E\xi)^2 = E(\xi^2) - E(\xi)^2$ 方差性质:
- $Var(c\xi+b) = c^2Var(\xi)$
- $Var\xi \leq E(\xi-c)^2$,等号成立当且仅当$c=E\xi$
- $Var(\sum_{i=1}^n \xi_i) = \sum_{i=1}^nVar\xi_i + 2\sum_{1\leq i,j\leq n}E(\xi_i-E\xi_i)(\xi_j-E\xi_j)$,特别地,如果它们两两独立,则有$Var(\sum_{i=1}^n \xi_i) = \sum_{i=1}^nVar\xi_i$
称$\xi^* = \frac{\xi-E\xi}{\sqrt{Var\xi}}$为$\xi$的标准化,期望为0,方差为1.
例:两两独立的n个正态分布的和仍服从正态分布:$c_0+c_1X_1+\cdots+c_nX_n \sim N(c_0+c_1\mu_1+\cdots+c_n\mu_n,c_1^2\sigma_1^2+\cdots+c_n^2\sigma_n^2)$
协方差$Cov(X,Y)=E(X-EX)(Y-EY) = E(XY)-E(X)E(Y)$ 协方差性质:
- $Cov(X,Y)=Cov(Y,X), Cov(X,a)=0$
- $Cov(X,X)=Var(X)$
- $Cov(aX,bY)=abCov(X,Y)$
- $Cov(X_1+X_2,Y) =Cov(X_1,Y)+Cov(X_2,Y)$
- $X,Y$独立可以推出$Cov(X,Y)=0$,反过来不一定
- $Var(X)Var(Y)\neq 0$的时候$(Cov(X,Y))^2 \leq Var(X)Var(Y)$,等号成立当且仅当$\exists c_1,c_2, s.t. P(Y=c_1+c_2X) = 1$(严格线性关系)
相关系数$\rho_{XY} = \frac{Cov(X,Y)}{\sqrt{Var(X)Var(Y)}}, |\rho_{XY}| \leq 1.$ 相关系数性质:
- $X,Y$相互独立可以推出$\rho_{XY}=0$,反之不一定
- $|\rho_{XY}|\leq 1$,等号成立当且仅当X和Y有严格线性关系,也就是说$|\rho_{XY}|$反映的是$X$和$Y$的线性关系密切程度
- $\rho_{XY}>0$称为正相关,反之为负相关
- 若$\rho_{XY}=0$,称X和Y不相关
- $\rho_{XY} = 0 \Leftrightarrow E(XY)=E(X)E(Y) \Leftrightarrow Var(X+Y)=Var(X)+Var(Y)$
例题
相遇概率
两个人会在五点到六点的任意时间到达车站,他们会呆五分钟然后离开,他们每天遇到的概率是多少?
这道题画图最直接,最终概率就是$\frac{6060-2(0.55555)}{60*60} = \frac{23}{144}.$
三角形概率
将一个棍子切成三段,能组成一个正方形的概率是多少?
记两次切的位置分别为$x,y, x<y$,则有 \(\begin{align*} x+(y-x) > 1-y &\Rightarrow y>1/2 \\ x+(1-y) > y-x &\Rightarrow y<1/2+x \\ (y-x)+(1-y) > x \Rightarrow x < 1/2 \end{align*}\)
因此概率为$2\times \frac{1}{8} = \frac{1}{4}$,因为$x>y$是完全对称的情况。
矩生成函数
令$M(t) = E(e^{tX})$,则有$M^{n}(0)=E(X^n)$.
若$X \sim N(0,1)$,则 $M(t) = \int_{-\infty}^{\infty}e^{tx}\frac{1}{\sqrt{2\pi}}e^{-x^2/2}dx = e^{t^2/2}\int_{-\infty}^{\infty}\frac{1}{\sqrt{2\pi}}e^{-(x-t)^2/2}dx = e^{t^2/2}$
因此$M’(0) = 0, M’‘(0)=1, M^3(0)=0, M^4(0)=3.$
数面条
如果碗里面有100个面条,你拿起面条的两个端点将他们连在一起,持续做这件事直到没有端点,请计算圆圈的期望数量。
如果只有一根那就是1,两根的话有4个端点,有$C_4^2=6$种拿法,其中有两种是直接将各自圈起来,因此圆圈的期望数量为$E(f(2))=\frac{2}{6}\times (1+E(f(1))) + \frac{4}{6} \times E(f(1)) = \frac{1}{3} + E(f(1)) = 1 + \frac{1}{3}$
以此类推,可以发现$E(f(n)) = 1+\frac{1}{3}+\cdots+\frac{1}{2n-1}.$ 再用归纳法进行证明。
最优对冲比例
你买了一份A股票,现在你想卖出一些B股票来对冲,你应该卖多少来使得你的利润方差最小化?假设A、B股票回报方差为$\sigma_A^2,\sigma_B^2$,它们的相关系数为$\rho$.
我们要最小化$Var(r_A-hr_B) = \sigma_A^2 + h^2\sigma_B^2 - 2h\rho\sigma_A\sigma_B \Rightarrow h = \rho\frac{\sigma_A}{\sigma_B}.$
骰子游戏
每次掷骰子,你都要支付那个面的数值,如果转到4\5\6则可以再投一次,否则游戏停止,请问游戏的花费期望是多少。
$Y$记为第一次掷骰子的点数,$X$为花费,则有$E(X|Y\in{1,2,3}) = 2, E(X|Y\in{4,5,6}) = 5 + E(X)$,因此$E(X) =\frac{1}{2}(7+E(X)) \Rightarrow E(X)=7.$
卡牌游戏
你在一张一张翻扑克牌,翻到第一张Ace所需要翻的牌数期望是多少?
令$X_i=1$如果卡牌$i$在Ace之前被翻,否则为0,那么$E(X)=1+\sum_{i=1}^48E(X_i)$
注意$P(X_i=1)=\frac{1}{5}$,这里可以考虑是第i个牌随机插入到由4个Ace构成的队列中,只有放在队首才能够满足。
因此$E(X) = 1+ \frac{48}{5}$
随机变量的和
假设$X_1,\ldots,X_n$独立同分布于$(0,1)$上的均匀分布,$S_n=X_1+\cdots+X_n \leq 1$的概率是多少?
用归纳法证明$P(S_n\leq 1) = \frac{1}{n!}.$
$P(S_{n+1}\leq 1) = \int_{0}^1 f(X_{n+1})P(S_n\leq 1-X_{n+1})dX_{n+1}=\int_0^1 \frac{(1-X_{n+1})^n}{n!} =\frac{1}{(n+1)!}$
收集优惠券
现在盒子里有N种不同的优惠券。(每种有很多张,相当于抽取后又放回)
- 如果一个孩子想要集齐所有的优惠券,平均需要多少个? 令$X_i$为收集到$(i-1)$个不同类型后收集到第$i$种优惠券所需优惠券的数量,因此$X=X_1+\cdots+X_N$ 对于任意的$i$,已收集$i-1$种类型,获得一个新类型的概率为$1-\frac{i-1}{N}$,这就相当于一个概率为$1-\frac{i-1}{N}$的几何分布,因此$E(X_i)=\frac{N}{N-i+1}$, 可以得到$E(X)=\sum_{i=1}^NE(X_i)=\sum_{i=1}^N \frac{N}{N-i+1}.$
- 如果已经收集到n个优惠券,优惠券种类数的期望是多少? 这里引入 indicator random variables $I_i$,其中$I_i=1$如果第$i$个类型在这$n$个优惠券中,否则为0, 由此可以得到$Y=\sum_{i=1}^NI_i,$对于任意一个优惠券,它不是第$i$种优惠券的概率为$\frac{N-1}{N}$, 可以得到$P(I_i=0) = (\frac{N-1}{N})^n\Rightarrow E(I_i)=P(I_i=1) = 1-(\frac{N-1}{N})^n.$ 可以得到$E(Y)=\sum_{i=1}^NE(I_i)=N(1-(\frac{N-1}{N})^n).$
违约概率
合同A明年违约概率为50%,合同B为30%,请问至少一个合同违约的概率在什么范围内以及它们之间的相关系数在什么范围内?
至少一个合同违约的概率最大为80%(A违约B就不违约),最小为50%(A违约B就一定违约) $I_A=1$表示A会违约,则有$E(I_A)=0.5,Var(I_A)=0.25,E(I_B)=0.3, Var(I_B)=0.21$ \(\begin{align} P(I_A=1 \|\| I_B=1) &= E(I_A)+E(I_B)-E(I_AI_B) \\ &= E(I_A) + E(I_B) -(E(I_A)E(I_B)-Cov(I_A,I_B)) \\ &= 0.8-(0.15-\rho_{AB}\sigma_A\sigma_B) \\ &= 0.65 - \sqrt{0.21}/2 \rho_{AB} \end{align}\) $0.5 \leq 0.65-\sqrt{0.21}/2 \rho_{AB} \leq 0.8 \Rightarrow -\sqrt{3/7}\leq \rho_{AB} \leq \sqrt{3/7}.$
随机蚂蚁
略,记住蚂蚁相遇只需调换标签即可。